
已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
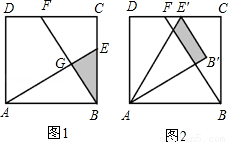
(1)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(2)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
(1)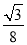 (2)没有变化
(2)没有变化
【解析】
试题分析:(1)先根据正方形的面积证出边长,然后根据相似三角形的判定得证△BGE∽△ABE,进而得出相似比和面积比,再根据勾股定理求得AE的长,求得△ABE的面积,根据面积的比求出△BGE的面积;
先根据正方形的面积求得边长,再由BE与AB的长求得∠BAE=30°,再根据据旋转变换的
∠B′AE′=30°,然后根据全等三角形判定SAS得出Rt△ABE≌Rt△AB′E′≌Rt△ADE′,因此∠DAE′=∠B′AE′=∠BAE=30°,且AE与AB′在同一直线上,然后根据ASA得证△BAG≌△HAG,从而得证结果.
试题解析:(1)【解析】
∵正方形面积为3,
∴AB=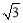
在△BGE与△ABE中,
∵∠GBE=∠BAE,∠EGB=∠EBA=90°,
∴△BGE∽△ABE
∴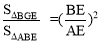
又∵BE=1,
∴AE2=AB2+BE2=3+1=4
∴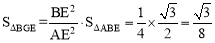
【解析】
没有变化。理由如下:
∵AB=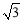 ,BE=1,
,BE=1,
∴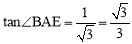
∴∠BAE=30°
∵AB′=AD,∠AB′E′=∠ADE'=90°,AE′= AE′,
∴Rt△ABE≌Rt△AB′E′≌Rt△ADE′,
∴∠DAE′=∠B′AE′=∠BAE=30°
∴AB′与AE在同一直线上,即BF与AB′的交点是G
设BF与AE′的交点为H,
则∠BAG=∠HAG=30°,而∠AGB=∠AGH=90°,AG= AG,
∴△BAG≌△HAG。
∴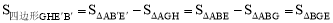
∴△ABE在旋转前后与△BCF重叠部分的面积没有变化
考点:相似三角形的判定与性质,全等三角形的判定与性质,三角形的面积


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系 中,正比例函数
中,正比例函数 与反比例函数
与反比例函数 的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.
的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.

(1)求反比例函数的解析式;
(2)若点P是反比例函数 图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:填空题
已知反比例函数 (k是常数,且
(k是常数,且 )的图象在第二、四象限,请写出一个符合条件的反比例函数表达式 .
)的图象在第二、四象限,请写出一个符合条件的反比例函数表达式 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市大兴区九年级上学期期末考试数学试卷(解析版) 题型:解答题
将表示下列事件发生的概率的字母标在下图中:

(1)投掷一枚骰子,掷出7点的概率 ;
;
(2)在数学测验中做一道四个选项的选择题(单选题),由于不知道那个是正确选项,现任选一个,做对的概率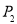 ;
;
(3)袋子中有两个红球,一个黄球,从袋子中任取一球是红球的概率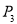 ;
;
(4)太阳每天东升西落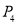 ;
;
(5)在1---100之间,随机抽出一个整数是偶数的概率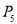 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市大兴区九年级上学期期末考试数学试卷(解析版) 题型:填空题
点A(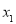 ,
,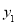 )、B(
)、B(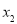 ,
,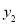 )在二次函数
)在二次函数 的图象上,若
的图象上,若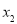 >
>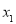 >1,则
>1,则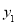 与
与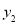 的大小关系是
的大小关系是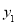
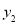 .(用“>”、“<”、“=”填空)
.(用“>”、“<”、“=”填空)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市朝阳区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,甲船在港口P的南偏东60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度驶向港口P;乙船从港口P出发,沿南偏西45°方向驶离港口P.现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向,求乙船的航行距离( ,
,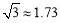 ,结果保留整数).
,结果保留整数).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市昌平区九年级上学期期末考试数学试卷(解析版) 题型:选择题
下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.等腰直角三角形 C.正方形 D.正五边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com