
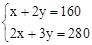 ,解得:
,解得: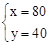 。
。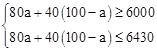 ,解得:
,解得: 。
。

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 ,放入一个大球水面升高
,放入一个大球水面升高  ;
; ,应放入大球、小球各多少个?
,应放入大球、小球各多少个?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | A元素含量 | 单价(万元/吨) |
| 甲原料 | 5% | 2.5 |
| 乙原料 | 8% | 6 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
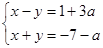 的解x为非正数,y 为负数.
的解x为非正数,y 为负数.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,
, ,
, ,
, . 例如:明文1,2,3,4对应的密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
. 例如:明文1,2,3,4对应的密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )| A.4,6,1,7 | B.4,1,6,7 | C.6,4,1,7 | D.1,6,4,7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com