
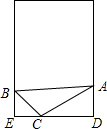
 小明将斜边AB=1米的直角三角形按图所示放置,其中∠BAC=30°,∠ACB=90°,∠ACD=37°,请你帮小明计算此门的宽度DE(参考数据:sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.73,结果精确到0.01米)
小明将斜边AB=1米的直角三角形按图所示放置,其中∠BAC=30°,∠ACB=90°,∠ACD=37°,请你帮小明计算此门的宽度DE(参考数据:sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.73,结果精确到0.01米) 分析 首先求出EC的长,即可利用锐角三角函数关系得出AC,CD的长,进而得出答案.
解答 解:∵∠BAC=30°,∠ACB=90°,AB=1米,
∴BC=$\frac{1}{2}$AB=0.5米,
又∵∠ACD=37°,
∴∠ECB=∠ACD=37°,
∴CE=BC•sin37°≈0.5×0.6=0.3(米).
∵AC=ABcos30°=$\frac{\sqrt{3}}{2}$≈0.865(米),
CD=ACcos37°≈0.692(米),
DE=0.3+0.992+0.08×2=1.152≈1.2(米),
答:门框的外宽度DE为1.2米.
点评 此题主要考查了解直角三角形的应用,根据题意熟练利用锐角三角函数关系是解题关键.


科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
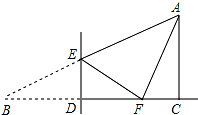 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6,点D是BC边上一动点(不与B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为直角三角形时,BD的长为1或2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com