
【题目】如图,已知ABCD是菱形,△EFP的顶点E,F,P分别在线段AB,AD,AC上,且EP=FP.
(1)证明:∠EPF+∠BAD=180°;
(2)若∠BAD=120°,证明:AE+AF=AP;
(3)若∠BAD=θ,AP=a,求AE+AF.

【答案】(1)证明见解析;(2)证明见解析;(3)AF+AE=PAcos![]() .
.
【解析】试题分析:(1)作PM⊥AD于M,PN⊥AC于N,Rt△PMF≌Rt△PNE,利用公共角求得∠MPF=∠NPE,可得∠EPF和∠BAD互补.
(2)按照(1)可得 Rt△PAM≌Rt△PAN,∠BAD=120°,所以可以得∠PAM=60°,易知PA=2AM,
AE+AF=PA.
(3)利用(1)(2)的方法,Rt△PMF≌Rt△PNE,可以得到AF+AE=(AM+FM)+(AN﹣EN)=2AM∠PAM=![]() ,易知AM=PAcos
,易知AM=PAcos![]() ,所以AF+AE=PAcos
,所以AF+AE=PAcos![]() .
.
试题解析:
(1)如图1中,作PM⊥AD于M,PN⊥AC于N.
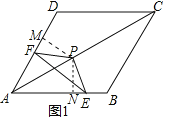
∵四边形ABCD是菱形,
∴∠PAM=∠PAN,
∴PM=PN,
∵PE=PF,
∴Rt△PMF≌Rt△PNE,
∴∠MPF=∠NPE,
∴∠EPF=∠MPF,
∵∠BAD+∠MPN=360°﹣∠AMP﹣∠ANP=180°,
∴∠EPF+∠BAD=180°.
(2)如图2中,作PM⊥AD于M,PN⊥AC于N.
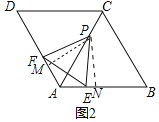
由(1)可知Rt△PMF≌Rt△PNE,
∴FM=NE,
∵PA=PA,PM=PN,
∴Rt△PAM≌Rt△PAN,
∴AM=AN,
∴AF+AE=(AM+FM)+(AN﹣EN)=2AM,
∵∠BAD=120°,
∴∠PAM=60°,易知PA=2AM,
∴AE+AF=PA.
(3)结论:AF+AE=PAcos![]() .
.
理由:如图2中,作PM⊥AD于M,PN⊥AC于N.
由(1)可知Rt△PMF≌Rt△PNE,
∴FM=NE,
∵PA=PA,PM=PN,
∴Rt△PAM≌Rt△PAN,
∴AM=AN,
∴AF+AE=(AM+FM)+(AN﹣EN)=2AM,
∵∠BAD=θ,
∴∠PAM=![]() ,易知AM=PAcos
,易知AM=PAcos![]() ,
,
∴AF+AE=PAcos![]() ./span>
./span>


科目:初中数学 来源: 题型:
【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是直角三角形时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是___时,它们一定不全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①若mx=my,则mx-my=0;
②若mx=my,则x=y;
③若mx=my,则mx+my=2my;
④若x=y,则mx=my.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com