
分析 根据每一项分别是12、22、32、42、52可找到规律,整理可得原式关于n的一个函数式,即可解题.
解答 解:12+22+32+42+52+…+292+…+n2
=0×1+1+1×2+2+2×3+3+3×4+4+4×5+5+…(n-1)n+n
=(1+2+3+4+5+…+n)+[0×1+1×2+2×3+3×4+…+(n-1)n]
=$\frac{n(n+1)}{2}$+{$\frac{1}{3}$(1×2×3-0×1×2)+$\frac{1}{3}$(2×3×4-1×2×3)+$\frac{1}{3}$(3×4×5-2×3×4)+…+$\frac{1}{3}$[(n-1)•n•(n+1)-(n-2)•(n-1)•n]}
=$\frac{n(n+1)}{2}$+$\frac{1}{3}$[(n-1)•n•(n+1)]
=$\frac{n(n+1)(2n+1)}{6}$,
∴当n=29时,原式=$\frac{29×(29+1)×(2×29+1)}{6}$=8555.
故答案为 8555.
点评 本题考查了学生发现规律并且整理的能力,本题中整理出原式关于n的解析式是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
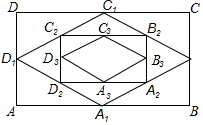 由四边形四条边的中点组成的四边形叫做原四边形的中点四边形.如图,四边形ABCD是矩形,取矩形ABCD四条边的中点得到中点四边形A1B1C1D1,再取四边形A1B1C1D1四条边的中点得到中点四边形A2B2C2D2,…,按此规律继续下去,若矩形ABCD的面积为1,则得到的中点四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.
由四边形四条边的中点组成的四边形叫做原四边形的中点四边形.如图,四边形ABCD是矩形,取矩形ABCD四条边的中点得到中点四边形A1B1C1D1,再取四边形A1B1C1D1四条边的中点得到中点四边形A2B2C2D2,…,按此规律继续下去,若矩形ABCD的面积为1,则得到的中点四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=24(1-a%-b%) | B. | m=24(1-a%)b% | C. | m=24-a%-b% | D. | m=24(1-a%)(1-b%) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a≠b,则a2≠b2 | B. | 若a>|b|,则a>b | C. | 若|a|=|b|,则a=b | D. | 若|a|>|b|,则a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com