
分析 由△=16(m+3)2-4×4(m2+6m)=144>0,于是得到函数图象与x轴恒有两个交点A,B,设A(x1,0),B(x2,0),于是得到|AB|=|x1-x2|=3.
解答 解:∵函数y=4x2-4(m+3)x+m2+6m,
∴△=16(m+3)2-4×4(m2+6m)=144>0,
∴函数图象与x轴恒有两个交点A,B,
设A(x1,0),B(x2,0),
∴|AB|=|x1-x2|=$\sqrt{({x}_{1}-{x}_{2})^{2}}$=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(m+3)^{2}-({m}^{2}+6m)}$=3.
点评 本题考查了抛物线与x轴的两交点之间的距离,熟练掌握抛物线与x轴的两交点之间的距离公式是解题的关键.


科目:初中数学 来源: 题型:选择题
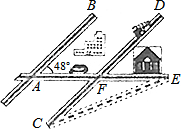 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )| A. | 48° | B. | 40° | C. | 30° | D. | 24° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | -5 | C. | 7 | D. | -7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 星期日,小英与小平同时从家里出发返回学校,速度分别为3千米/小时,4千米/小时,小平家离学校18千米,小英家在小平返校的路上,离小平家2千米.
星期日,小英与小平同时从家里出发返回学校,速度分别为3千米/小时,4千米/小时,小平家离学校18千米,小英家在小平返校的路上,离小平家2千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
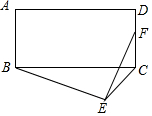 如图,在矩形ABCD中,AB=5,AD=12,以BC为斜边在矩形外部作直角三角形BEC,F为CD的中点,则EF的最大值为( )
如图,在矩形ABCD中,AB=5,AD=12,以BC为斜边在矩形外部作直角三角形BEC,F为CD的中点,则EF的最大值为( )| A. | $\frac{\sqrt{433}}{2}$ | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | $\frac{\sqrt{433}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
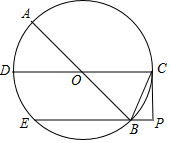 如图,AB、CD是⊙O的直径,BE是⊙O的弦,且BE∥CD,过点C的切线与EB的延长线交于点P,连接BC.
如图,AB、CD是⊙O的直径,BE是⊙O的弦,且BE∥CD,过点C的切线与EB的延长线交于点P,连接BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com