
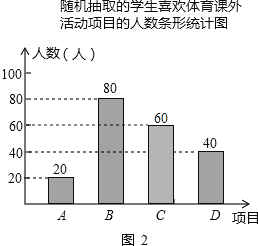
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有人;
(2)请你将条形统计图补充完成;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
【答案】
(1)200
(2)
解:C项目对应人数为:200﹣20﹣80﹣40=60(人);
补充如图.
(3)
解:列表如下:
甲 | 乙 | 丙 | 丁 | |
甲 | ﹨ | (乙,甲) | (丙,甲) | (丁,甲) |
乙 | (甲,乙) | ﹨ | (丙,乙) | (丁,乙) |
丙 | (甲,丙) | (乙,丙) | ﹨ | (丁,丙) |
丁 | (甲,丁) | (乙,丁) | (丙,丁) | ﹨ |
∵共有12种等可能的情况,恰好选中乙、丙两位同学的有2种,
∴P(选中甲、乙)= ![]() =
= ![]()
【解析】解:(1)根据题意得:这次被调查的学生共有20÷ ![]() =200(人).
=200(人).
故答案为:200;
(1)由题意可知这次被调查的学生共有20÷ ![]() =200(人);(2)首先求得C项目对应人数为:200﹣20﹣80﹣40=60(人),继而可补全条形统计图;(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案.此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.
=200(人);(2)首先求得C项目对应人数为:200﹣20﹣80﹣40=60(人),继而可补全条形统计图;(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案.此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:
【题目】为保证中小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的统计 图(1)和图(2).
(1)请根据所给信息在图(1)中将表示“乒乓球”项目的图形补充完整;
(2)扇形统计图(2)中表示”足球”项目扇形的圆心角度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AC⊥AB,AB=2 ![]() ,AC=2,点D是以AB为直径的半圆O上一动点,DE⊥CD交直线AB于点E,设∠DAB=α(0°<α<90°).
,AC=2,点D是以AB为直径的半圆O上一动点,DE⊥CD交直线AB于点E,设∠DAB=α(0°<α<90°). 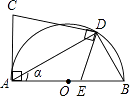
(1)当α=18°时,求 ![]() 的长;
的长;
(2)当α=30°时,求线段BE的长;
(3)若要使点E在线段BA的延长线上,则α的取值范围是(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30°,再向旗杆的方向前进16米,到达点D处(C、D、B三点在同一直线上),又测得旗杆顶端A的仰角为45°,请计算旗杆AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=(用α表示);如图②,∠CBO= ![]() ∠ABC,∠BCO=
∠ABC,∠BCO= ![]() ∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
(2)如图③,∠CBO= ![]() ∠DBC,∠BCO=
∠DBC,∠BCO= ![]() ∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO= ![]() ∠DBC,∠BCO=
∠DBC,∠BCO= ![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Pn表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么Pn与n的关系式是:Pn= ![]() (n2﹣an+b)(其中a,b是常数,n≥4)
(n2﹣an+b)(其中a,b是常数,n≥4)
(1)通过画图,可得:四边形时,P4= ;五边形时,P5=
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区7月1日﹣7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:
(1)随机选择一天,恰好天气预报是晴;
(2)随机选择连续的两天,恰好天气预报都是晴.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com