Question

13．如图，已知二次函数y=ax²+bx+2的图象过A（-1，0）和B（5，-3）两点．
（1）求二次函数的解析式；
（2）设二次函数的图象与x轴的另一个交点为C，求点C的坐标；
（3）二次函数的图象与y轴的交点为D，点E在第一象限内二次函数的图象上，点F在线段CD上，当△ACD∽△FDE时，求EF的长．

Answer 1

分析 （1）利用待定系数法即可解决问题．
（2）令y=0，解方程即可解决．
（3）首先证明△ADC是直角三角形，作DE∥OC交抛物线于E，作EF⊥DE，交CD于F，可以证明△ACD∽△FDE，利用相似三角形的性质，列出方程即可解决问题．

解答 解：（1）∵二次函数y=ax²+bx+2的图象过A（-1，0）和B（5，-3）两点，
∴$\left\{\begin{array}{l}{a-b+2=0}\\{25a+5b+2=-3}\end{array}\right.$，
∴$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$，
∴二次函数的解析式y=-$\frac{1}{2}$x²+$\frac{3}{2}$x+2．

（2）令y=0，则有-$\frac{1}{2}$x²+$\frac{3}{2}$x+2=0，
∴x²-3x-4=0，
∴（x-4）（x+1）=0，
∴x=4或-1，
∴点C坐标（4，0）．

（3）∵OD=2，OA=1，OB=4，
∴OD²=OA•OB，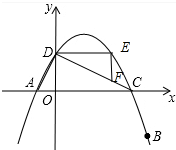
∴$\frac{OD}{OA}$=$\frac{OB}{OD}$，
∵∠DOA=∠DOC=90°，
∴△DOA∽△COD，
∴∠ADO=∠DCO，
∵∠DCO+∠ODC=90°，
∴∠ADO+∠ODC=90°，
∴∠ADC=90°，
作DE∥OC交抛物线于E，作EF⊥DE，交CD于F．
∵∠EDF=∠ACD，∠DEF=∠ADC，
∴△ACD∽△FDE，
∵点E坐标（3，2），
∴DE=3，
∵$\frac{DE}{DC}$=$\frac{EF}{AD}$，
∴$\frac{3}{2\sqrt{5}}$=$\frac{EF}{\sqrt{5}}$，
∴EF=$\frac{3}{2}$．

点评 本题考查二次函数的综合题、待定系数法、相似三角形的判定和性质，解题的关键是发现△ADC是直角三角形，学会用方程的思想思考问题，属于中考压轴题．