A
分析:根据四边形ABCD的四边都相等得出菱形ABCD,根据菱形的性质推出∠B=∠D,∠A=∠C,AD∥BC,根据平行线的性质得出∠DAB+∠B=180°,根据等边三角形的性质得出∠AEF=∠AFE=60°,AF=AD,根据等边对等角得出∠B=∠AEB,∠D=∠AFD,设∠BAE=∠FAD=x,根据三角形的内角和定理得出方程x+2(180°-60°-2x)=180°,求出方程的解即可求出答案.
解答:∵四边形ABCD的四边都相等,
∴四边形ABCD是菱形,
∴∠B=∠D,∠A=∠C,AD∥BC,
∴∠DAB+∠B=180°,
∵△AEF是等边三角形,AE=AB,
∴∠AEF=∠AFE=60°,AF=AD,
∴∠B=∠AEB,∠D=∠AFD,
由三角形的内角和定理得:∠BAE=∠FAD,
设∠BAE=∠FAD=x,
则∠D=∠AFD=180°-60°-2x,
∵∠FAD+∠D+∠AFD=180°,
∴x+2(180°-60°-2x)=180°,
解得:x=20°,
∴∠C=∠BAD=2×20°+60°=100°,
故选A.
点评:本题主要考查对菱形的判定和性质,等边三角形的性质,等腰三角形的性质,三角形的内角和定理,平行线的性质等知识点的理解和掌握,设∠BAE=∠FAD=x,根据这些性质得出∠D=∠AFD=180°-60°-2x是解此题的关键,题型较好,难度适中.

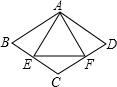 如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=
如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=

 阅读快车系列答案
阅读快车系列答案
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且
