
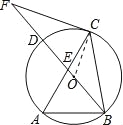
【题目】如图,△ABC内接于⊙O,∠A=60°,点F是直径BD的延长线上一点,且CF=CB.
(1)求∠CBF的度数;
(2)判断直线CF与⊙O的位置关系,并证明;
(3)若AB=3,BC=2![]() ,tan∠AEB=3,求线段DE的长.
,tan∠AEB=3,求线段DE的长.

【答案】(1)∠CBF=30°;
(2)CF是⊙O的切线,证明见解析;
(3)![]() .
.
【解析】
试题分析:(1)连接OA,根据圆周角定理求出∠BOC,再由OB=OC得出∠OBC=∠OCB=30°,从而求得∠CBF的度数;
(2)由CF=CB得出∠F=30°,进而求得∠BCF=120°,继而由∴∠OCF=∠BCF﹣∠OCB=90°,可得出OC⊥FC,从而得出CF是⊙O的切线.
(3)作BG⊥AC于G,CH⊥BF于H,根据直角三角函数和勾股定理求得AE、BE、CE,然后根据相交弦定理就可求得DE的长.
试题解析:(1)连接OC,∵∠A=60°,∴∠BOC=2∠A=120°,又∵OB=OC,
∴∠OBC=∠OCB=30°,即∠CBF=30°.
(2)相切;
理由如下:∵CF=CB,∴∠CBF=∠F=30°,∴∠BCF=120°,
∴∠OCF=∠BCF﹣∠OCB=90°,∴OC⊥FC,∴CF是⊙O的切线.
(3)作BG⊥AC于G,CH⊥BF于H,∵∠A=60°,AB=3,
∴AG=![]() AB=
AB=![]() ,BG=
,BG=![]() AB=
AB=![]() ,∵tan∠AEB=3,∴
,∵tan∠AEB=3,∴![]() =3,
=3,
∴EG=![]() =
=![]() ,∴AE=AG+GE=
,∴AE=AG+GE=![]() ,∴BE=
,∴BE=![]() =
=![]() ,
,
∵∠FBC=30°,BC=2![]() ,∴HC=
,∴HC=![]() BC=
BC=![]() ,∵tan∠AEB=3,,∴tan∠HEC=3,
,∵tan∠AEB=3,,∴tan∠HEC=3,
∴![]() =3,,∴HE=
=3,,∴HE=![]() ,∴EC=
,∴EC=![]() =
=![]() ,∵DE×BE=CE×AE,
,∵DE×BE=CE×AE,
∴DE=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】2017年6月13日,2016——2017赛季NBA总决赛第五场金州勇士队129:120战胜克利夫兰骑士队,赢得了总冠军,凯文·杜兰特表现抢眼,荣膺总决赛MVP,总决赛中凯文·杜兰特和勒布朗·詹姆斯每场得分数据如下:
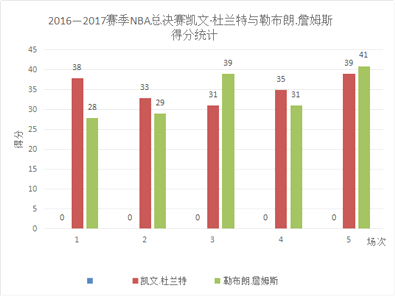
(1)求两名队员得分数的平均数.
(2)求凯文·杜兰特五场比赛得分的中位数.
(3)篮球迷小明同学已经求出了勒布朗·詹姆斯五场得分的方差为S2=28.64,凯文·杜兰特五场比赛得分的方差为S2=8.96,请帮他说明哪位运动员发挥更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列抛物线中,与x轴有两个交点的是( )
A. y=3x2-5x+3 B. y=4x2-12x+9 C. y=x2-2x+3 D. y=2x2+3x-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着IT技术的普及,越来越多的学校开设了微机课.某初中计划拿出72万元购买电脑,由于团体购买,结果每台电脑的价格比计划降低了500元,因此实际支出了64万元.实际每台电脑的价格为多少元?若每台电脑每天最多可使用4节课,这些电脑每天最多可供多少学生上微机课?(该校上微机课时规定为单人单机)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中,移项正确的是( )
A. 由x-3=4得x=4-3
B. 由2=3+x得2-3=x
C. 由3-2x=5+6得2x-3=5+6
D. 由-4x+7=5x+2得5x-4x=7+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张掷一枚硬币,结果是一连9次掷出正面向上,那么他第10次掷硬币时,出现正面向上的概率是( ).
A. 0 B. 1 C. 0.5 D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com