
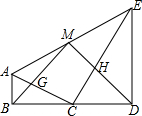
 已知:如图,Rt△CDE中,∠ABC=∠CDE=90°,且BC与CD共线,联结AE,点M为AE中点,联结BM,交AC于点G,联结MD,交CE于点H
已知:如图,Rt△CDE中,∠ABC=∠CDE=90°,且BC与CD共线,联结AE,点M为AE中点,联结BM,交AC于点G,联结MD,交CE于点H分析 (1)延长BM交DE的延长线于N,如图,根据平行线分线段成比例定理,由AB∥DN得到$\frac{BM}{MN}$=$\frac{AM}{ME}$,加上AM=ME,则BM=MN,然后根据直角三角形斜边上的中线性质即可得到MB=MD;
(2)根据平行线分线段成比例定理,由AB∥NE得到$\frac{AB}{NE}$=$\frac{AM}{ME}$=1,即AB=NE,再利用AB=BC,DC=DE可得BD=DN,则△BDN为等腰直角三角形,所以DM⊥BN,∠DBN=∠N=45°,∠BMD=90°,接着由Rt△ABC和Rt△CDE都是等腰直角三角形得到∠CED=∠ACB=∠45°,则可得到CE∥BN,AC∥DM,于是可判断四边形MGCH为平行四边形,加上∠GMH=90°,则可判断四边形MGCH为矩形.
解答 证明:(1)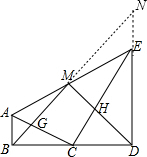 延长BM交DE的延长线于N,如图,
延长BM交DE的延长线于N,如图,
∵∠ABC=∠CDE=90°,
∴AB∥DN,
∴$\frac{BM}{MN}$=$\frac{AM}{ME}$,
而点M为AE中点,
∴AM=ME,
∴BM=MN,
∴DM为Rt△BDN的斜边上的中线,
∴MB=MD;
(2)∵AB∥NE,
∴$\frac{AB}{NE}$=$\frac{AM}{ME}$=1,即AB=NE,
∵AB=BC,DC=DE,
∴BD=BC+CD=AB+DE=NE+DE=DN,
∴△BDN为等腰直角三角形,
∴DM⊥BN,∠DBN=∠N=45°,∠BMD=90°,
∵AB=BC,DC=DE,
∴Rt△ABC和Rt△CDE都是等腰直角三角形,
∴∠CED=∠ACB=∠45°,
∴∠CED=∠N,∠ACB=∠BDM,
∴CE∥BN,AC∥DM,
∴四边形MGCH为平行四边形,
而∠GMH=90°,
∴四边形MGCH为矩形.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.也考查了矩形的判定和等腰直角三角形的性质.


科目:初中数学 来源: 题型:填空题
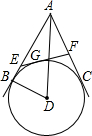 如图所示,⊙D 的半径为3,A是圆D外一点且AD=5,AB,AC分别与⊙D相切于点B,C.G是劣弧BC上任意一点,过G作⊙D的切线,交AB于点E,交AC于点F.
如图所示,⊙D 的半径为3,A是圆D外一点且AD=5,AB,AC分别与⊙D相切于点B,C.G是劣弧BC上任意一点,过G作⊙D的切线,交AB于点E,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如下表:
假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如下表:| 单价/(元/千克) | 4 | 3 | 2 | 合计 |
| 小红购买的数量/千克 | 1 | 2 | 3 | 6 |
| 小慧购买的数量/千克 | 2 | 2 | 2 | 6 |
| 每次购买单价相同,购买总量也相同,平均价格应该也一样,都是(4+3+2)÷3=3(元/千克),所以两人购买的西红柿一样便宜. |
| 购买的总量虽然相同,但小红花了16元,小慧花了18元,平均价格不一样,所以购买的西红柿便宜 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
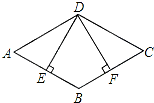 如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.| A. | 16$\sqrt{3}$ | B. | 64 | C. | 8$\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -9 | B. | -1 | C. | 5 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com