
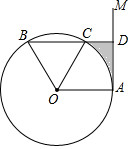
 如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.分析 (1)由已知条件得到△BOC是等边三角形,根据等边三角形的性质得到∠1=∠2=60°,由角平分线的性质得到∠1=∠3,根据平行线的性质得到∠OAM=90°,于是得到结论;
(2)根据等边三角形的性质得到∠OAC=60°,根据三角形的内角和得到∠CAD=30°,根据勾股定理得到AD=2$\sqrt{3}$,于是得到结论.
解答 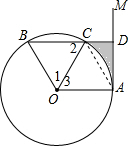 解:(1)∵∠B=60°,
解:(1)∵∠B=60°,
∴△BOC是等边三角形,
∴∠1=∠2=60°,
∵OC平分∠AOB,
∴∠1=∠3,
∴∠2=∠3,
∴OA∥BD,
∴∠BDM=90°,∴∠OAM=90°,
∴AM是⊙O的切线;
(2)∵∠3=60°,OA=OC,
∴△AOC是等边三角形,
∴∠OAC=60°,
∵∠OAM=90°,
∴∠CAD=30°,
∵CD=2,
∴AC=2CD=4,
∴AD=2$\sqrt{3}$,
∴S阴影=S梯形OADC-S扇形OAC=$\frac{1}{2}$(4+2)×2$\sqrt{3}$-$\frac{60•π×16}{360}$=6$\sqrt{3}$-$\frac{8π}{3}$.
点评 本题考查了切线的判定和性质,等边三角形的性质和判定,平行线的性质,正确的作出辅助线是解题的关键.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:选择题
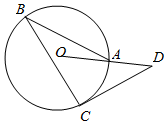 如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )| A. | 29° | B. | 32° | C. | 42° | D. | 58° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )| A. | 1.8 | B. | 2.4 | C. | 3.2 | D. | 3.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-7x}$ | B. | $\sqrt{-199{9x}^{3}}$ | C. | $\sqrt{{-0.1x}^{2}-1}$ | D. | $\root{3}{-{6x}^{2}-5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
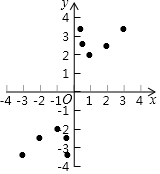 某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:
某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{10}{3}$ | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com