练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．已知圆锥的高是3cm，母线长5cm，则圆锥的侧面积是20πcm2．（结果保留π）．

    分析 首先利用勾股定理求得圆锥的底面半径，然后利用圆锥的侧面积=π×底面半径×母线长，把相应数值代入即可求解．

    解答 解：∵圆锥的高是3cm，母线长5cm，
    ∴勾股定理得圆锥的底面半径为4cm，
    ∴圆锥的侧面积=π×4×5=20πcm2．
    故答案为：20π．

    点评 本题考查圆锥侧面积公式的运用，掌握公式是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．某商品进价为80元，按进价提高50%后标价，打折销售后仍可获利20%，问此商品打的折数是八．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

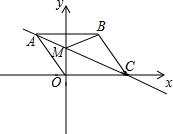    9．已知：如图平面直角坐标系xOy中，C在x轴上，四边形OABC为菱形，且A点坐标
    为（-3，4），过A、C的直线交y轴于点M，连接BM
    （1）求直线AC的解析式
    （2）一动点P从A出发，以每秒2个单位长度沿A→B→C向C点运动，设运动过程中△PBM的面积为S，运动时间为t（秒），试求出S关于t的函数关系式．
    （3）在（2）的条件下，试求出当t为何值时，△PBM的面积的最大值？最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知：如图，△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90°，D为AB边上一点，求∠EAC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

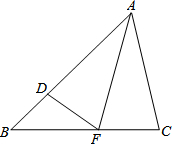    13．如图，在△ABC中，AB＞AC，AF是∠BAC的平分线，D是AB上一点，AD=AC．
    （1）△ADF与△ACF全等吗？为什么？
    （2）又过D作DE∥BC交AC于点E，连接CD，请你补全图形，并说明CD是否会平分∠FDE？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．2014年12月26日，南宁至广州高速铁路开始运行，从南宁到广州，乘空调快车的行程为872km，高铁开通后，高铁列车的行程约为580km，运行时间比空调快车时间少了8h．若高铁列车的平均速度是空调快车的2.5倍，求高铁列车的平均速度．设空调快车平均速度为xkm/h，则根据题意所列方程正确的是（　　）
    A．$\frac{580}{2.5x}=\frac{872}{x}-8$B．$\frac{580}{2.5x}=\frac{872}{x}+8$C．$\frac{580}{x}=\frac{872}{2.5x}-8$D．$\frac{580}{x}=\frac{872}{2.5x}+8$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

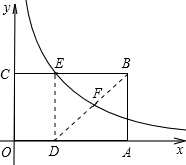    10．如图，在矩形OABC中，OA、OC两边分别在x轴y轴的正半轴上，OA=3，OC=2，过OA边上的D点，沿着BD翻折△ABD，点A恰好落在BC边上的点E处，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点E与BD相交于点F，抛物线y=ax2+bx+2经过点E、F．
    （1）求反比例函数的解析式；
    （2）求抛物线的解析式；
    （3）连接OE、OF、EF，点M是抛物线上一动点，是否存在点M，使△MOE的面积与△OEF相等？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

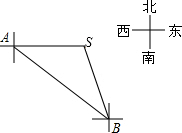    7．为维护南海主权，我海军舰艇加强对南海海域的巡航，2015年4月10日上午9时，我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S，该舰艇沿南偏东45°的方向航行，11时到达观察点B，测得灯塔S位于其北偏西15°方向，求该舰艇的巡航速度？（结果保留整数）
    （参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．宝应县2015年3月的一天最高气温为21℃，最低气温为-1℃，则这天的最高气温比最低气温高22℃．

    查看答案和解析>>

    同步练习册答案