
 ��ͼ���ھ���OABC�У�OA��OC���߷ֱ���x��y����������ϣ�OA=3��OC=2����OA���ϵ�D�㣬����BD���ۡ�ABD����Aǡ������BC���ϵĵ�E��������������y=$\frac{k}{x}$��x��0����ͼ����E��BD�ཻ�ڵ�F��������y=ax2+bx+2������E��F��
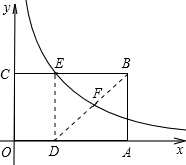
��ͼ���ھ���OABC�У�OA��OC���߷ֱ���x��y����������ϣ�OA=3��OC=2����OA���ϵ�D�㣬����BD���ۡ�ABD����Aǡ������BC���ϵĵ�E��������������y=$\frac{k}{x}$��x��0����ͼ����E��BD�ཻ�ڵ�F��������y=ax2+bx+2������E��F������ ��1�����E�����꣬���뷴������������ʽ���ɣ�
��2�����BD����ʽ�����y=$\frac{2}{x}$��ɷ����飬���F�����꣬��E��1��2����F��2��1���ֱ�������ʽ���ú�������ʽΪy=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2��
��3����OM��EF�����OM����ʽ�õ�M�����꣬���OF��EM����ʽ���ж���OF��EM���õ��ı���OFEMΪƽ���ı��Σ���MOE��������OEF��ȣ���M��-1��1������y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2�ã�1=-1����M���������ϣ��������Mƽ����OE��ֱ���������ߵĽ��㣬�Լ�����Fƽ����OE��ֱ���������ߵĽ��㣬���ɽ�����⣮
��� �⣺��1���ɷ��ۿ�֪��AD=DE=OC=2��
��OD=3-2=1��E��������1��2����D��1��0����
k=1��2=2��
��������������ʽΪy=$\frac{2}{x}$��
��2����BD����ʽΪy=kx+b��
��B��3��2����D��1��0���ֱ�������ʽ�ã�$\left\{\begin{array}{l}3k+b=2\\ k+b=0\end{array}\right.$�����$\left\{\begin{array}{l}k=1\\ b=-1\end{array}\right.$��
�ʺ�������ʽΪy=x-1��
��y=$\frac{2}{x}$��y=x-1��ɷ�����ã�$\left\{\begin{array}{l}y=\frac{2}{x}\\ y=x-1\end{array}\right.$��
���x2-x-2=0��
x1=-1����ȥ����x2=2��
��F��������2��1����
��E��1��2����F��2��1���ֱ�������ʽ�ã�$\left\{\begin{array}{l}4a+2b+2=1\\ a+b+2=2\end{array}\right.$��
���$\left\{\begin{array}{l}a=-\frac{1}{2}\\ b=\frac{1}{2}\end{array}\right.$��
�ʺ�������ʽΪy=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2��
��3����EF����ʽΪy=ax+b��
��E��1��2����F��2��1���ֱ�������ʽ��$\left\{\begin{array}{l}2a+b=1\\ a+b=2\end{array}\right.$��
���$\left\{\begin{array}{l}a=-1\\ b=3\end{array}\right.$��
��������ʽΪy=-x+3��
��OM��EF��
��OM����ʽΪy=-x��
��y=-x��y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2��ɷ�����ã�$\left\{\begin{array}{l}y=-x\\ y=-\frac{1}{2}{x}^{2}+\frac{1}{2}x+2\end{array}\right.$��
���$\left\{\begin{array}{l}x=-1\\ y=1\end{array}\right.$��$\left\{\begin{array}{l}x=4\\ y=-4\end{array}\right.$���ᣩ��
��M��-1��1����
��OF����ʽΪy=mx����F��2��1�����������m=$\frac{1}{2}$��
�ʺ�������ʽΪy=$\frac{1}{2}$x��
����ME����ME����ʽΪy=dx+e��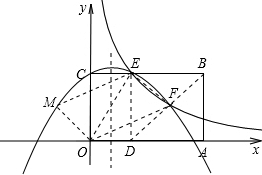
��M��-1��1����E��1��2���ֱ�������ʽ��$\left\{\begin{array}{l}-d+e=1\\ d+e=2\end{array}\right.$��
���$\left\{\begin{array}{l}d=\frac{1}{2}\\ e=\frac{3}{2}\end{array}\right.$��
��������ʽΪy=$\frac{1}{2}$x+$\frac{3}{2}$��
��֪OF��ME��
���ı���OFEMΪƽ���ı��Σ�
���MOE��������OEF��ȣ�
��M��-1��1������y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2�ã�1=-1����M���������ϣ�
����Mƽ����OE��ֱ��Ϊy=2x+3��
��$\left\{\begin{array}{l}{y=2x+3}\\{y=-\frac{1}{2}{x}^{2}+\frac{1}{2}x+2}\end{array}\right.$���$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$��
���M�����껹����Ϊ��-2��-1����
����Fƽ����OE��ֱ��Ϊy=2x-3��
��$\left\{\begin{array}{l}{y=2x-3}\\{y=-\frac{1}{2}{x}^{2}+\frac{1}{2}x+2}\end{array}\right.$���$\left\{\begin{array}{l}{x=2}\\{Y=1}\end{array}\right.$��$\left\{\begin{array}{l}{x=-5}\\{y=-13}\end{array}\right.$��
���M�����껹����Ϊ��-5��-13����
��M��-1��1������y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2�ã�1=-1����M���������ϣ�
����������M���꣨-1��1����-2��-1����-5��-13����
���� ���⿼���˷����������ۺ��⣬�漰����ϵ������һ�κ��������κ�������ʽ�����۱任��ƽ���ı��ε��ж������ʣ��ۺ���ǿ����һ�����⣮


 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
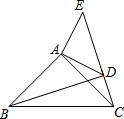 ��ͼ����ACB�͡�ADE���ǵ���ֱ�������Σ���BAC=��DAE=90�㣬��C��D��E������ͬһֱ���ϣ�����BD�����BDE=90�ȣ�
��ͼ����ACB�͡�ADE���ǵ���ֱ�������Σ���BAC=��DAE=90�㣬��C��D��E������ͬһֱ���ϣ�����BD�����BDE=90�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a+3b=5ab | B�� | ��-2a2��3=6a6 | C�� | a3•a2=a6 | D�� | -a5�£�-a��=a4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
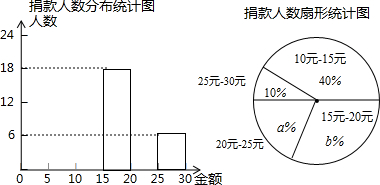
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com