
 以下要求写出必要的演算步骤.
以下要求写出必要的演算步骤. )-1,y=-2;
)-1,y=-2; )-1=2,y=-2时,原式=28-(-2)8=0;
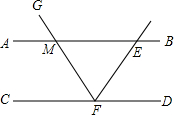
)-1=2,y=-2时,原式=28-(-2)8=0; ∠GFD=64°,
∠GFD=64°,

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
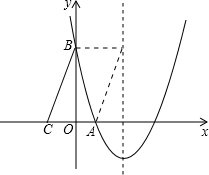 (-1,0),把△BOC向右平移2个单位长度后,一条直角边恰好在抛物线的对称轴上.
(-1,0),把△BOC向右平移2个单位长度后,一条直角边恰好在抛物线的对称轴上.查看答案和解析>>
科目:初中数学 来源: 题型:单选题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABDC中,AD平分∠BAC,DB=DC,
如图,四边形ABDC中,AD平分∠BAC,DB=DC,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com