
 如图,点O为 Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
如图,点O为 Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.分析 (1)由Rt△ABC中,∠C=90°,⊙O切BC于D,易证得AC∥OD,继而证得AD平分∠CAB.
(2)如图,连接ED,根据(1)中AC∥OD和菱形的判定与性质得到四边形AEDO是菱形,则△AEM≌△DMO,则图中阴影部分的面积=扇形EOD的面积.
解答 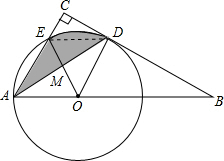 解:
解:
(1)证明:∵⊙O切BC于D,
∴OD⊥BC,
∵AC⊥BC,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠CAD,
即AD平分∠CAB;
(2)设EO与AD交于点M,连接ED.
∴∠B=30°,
∴∠BAC=60°,
∵OA=OE,
∴△AEO是等边三角形,
∴AE=OA,∠AOE=60°,
∴AE=AO=OD,
又由(1)知,AC∥OD即AE∥OD,
∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,
∴S△AEM=S△DMO,
∴S阴影=S扇形EOD=$\frac{60π×{2}^{2}}{360}$=$\frac{2}{3}$π.
点评 此题考查了切线的性质、扇形面积公式的运用、等腰三角形的性质以及等边三角形的判定和性质,熟记和圆有关的各种性质是解题的关键.


科目:初中数学 来源: 题型:解答题
 某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号)
某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
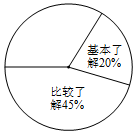 为纪念交通大学建校120周年进行宣传,附中中学某年级开展了主题为“交通大学历史知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了如图不完整的表格和扇形统计图.
为纪念交通大学建校120周年进行宣传,附中中学某年级开展了主题为“交通大学历史知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了如图不完整的表格和扇形统计图.| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 50 | m | 40 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
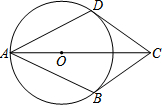 如图,已知在四边形ABCD中,AB=AD,BC=CD,点O在对角线AC上,以O为圆心OA为半径的⊙O与CD相切于点D.
如图,已知在四边形ABCD中,AB=AD,BC=CD,点O在对角线AC上,以O为圆心OA为半径的⊙O与CD相切于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com