练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，把一个多边形的一个顶点与其余各顶点连接起来，可以把这个多边形分割成若干个三角形.

    （1）把一个100边形的一个顶点与其余各顶点连接起来，一共可以连几条线段？

    （2）在（1）中，这些线段将100边形分割成几个三角形？

    【答案】(1)97 (2)98

    【解析】

    （1）观察四边形、五边形、六边形、七边形可知与这个顶点相邻的两个顶点之间的线段是多边形的边，因此可以推断出100边形的一个顶点与其余各顶点连接起来，一共可以连（100-3）条线段；

    （2）观察所给的图形可以得到（1）中的线段将100边形分割成（100-2）个三角形.

    （1）观察四边形一个顶点与其余顶点连接起来有1条线段，即1=4-3，

    五边形一个顶点与其余顶点连接起来有2条线段，即2=5-3，

    六边形一个顶点与其余顶点连接起来有3条线段，即3=6-3，

    七边形一个顶点与其余顶点连接起来有4条线段，即4=7-3，

    ……，

    所以n边形一个顶点与其余顶点连接起来有(n-3)条线段，

    100-3=97，

    所以100边形一个顶点与其余顶点连接起来有97条线段；

    （2）观察可知四边形一个顶点与其余顶点连接的线段将四边形分成2个小三角形，即2=4-2，

    五边形一个顶点与其余顶点连接的线段将五边形分成3个小三角形，即3=5-2，

    六边形一个顶点与其余顶点连接的线段将六边形分成4个小三角形，即4=6-2，

    七边形一个顶点与其余顶点连接的线段将七边形分成5个小三角形，即5=7-2，

    ……，

    所以，n边形一个顶点与其余顶点连接的线段将n边形分成（n-2）个小三角形，

    100-2=98，

    所以在（1）中，这些线段将100边形分割成98个三角形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：
    如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2=交于A（1，3）和B（﹣3，﹣1）两点．
    观察图象可知：
    ①当x=﹣3或1时，y1=y2；
    ②当﹣3＜x＜0或x＞1时，y1＞y2 ， 即通过观察函数的图象，可以得到不等式ax+b＞的解集．
    有这样一个问题：求不等式x3+4x2﹣x﹣4＞0的解集．
    某同学根据学习以上知识的经验，对求不等式x3+4x2﹣x﹣4＞0的解集进行了探究．

    下面是他的探究过程，请将（2）、（3）、（4）补充完整：
    （1）将不等式按条件进行转化：
    当x=0时，原不等式不成立；
    当x＞0时，原不等式可以转化为x2+4x﹣1＞；
    当x＜0时，原不等式可以转化为x2+4x﹣1＜；
    （2）构造函数，画出图象
    设y3=x2+4x﹣1，y4= ， 在同一坐标系中分别画出这两个函数的图象．
    双曲线y4=如图2所示，请在此坐标系中画出抛物线y3=x2+4x﹣1；（不用列表）
    （3）确定两个函数图象公共点的横坐标
    观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y3=y4的所有x的值为；
    （4）借助图象，写出解集
    结合（1）的讨论结果，观察两个函数的图象可知：不等式x3+4x2﹣x﹣4＞0的解集为．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．

    （1）计算AC2+BC2的值等于　 　；

    （2）请在如图所示的网格中，用无刻度的直尺，画出一个平行四边形ABEF，使得该平行四边形的面积等于16；

    （3）请在如图所示的网格中，用无刻度的直尺，画出一个矩形ABMN，使得该矩形的面积等于AC2+BC2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，O为坐标原点．直线y=kx+b与抛物线y=mx2﹣x+n同时经过A（0，3）、B（4，0）．
    （1）求m，n的值．
    （2）点M是二次函数图象上一点，（点M在AB下方），过M作MN⊥x轴，与AB交于点N，与x轴交于点Q．求MN的最大值．
    （3）在（2）的条件下，是否存在点N，使△AOB和△NOQ相似？若存在，求出N点坐标，不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了加强学生的安全意识，某校组织了学生参加安全知识竞赛．从中抽取了部分学生成绩（得分数取正整数，满分为100分）进行统计，已知A组的频数a比B组的频数b小24，绘制统计频数分布直方图（未完成）和扇形图如下，请解答下列问题：

    （1）样本容量为：______，a为______；

    （2）n为________，E组所占比例为________；

    （3）补全频数分布直方图；

    （4）若成绩在80分以上记作优秀，全校共有2000名学生，估计成绩优秀学生有_________名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为深化义务教育课程改革，某校积极开展拓展性课程建设，计划开设艺术、体育、劳技、文学等多个类别的拓展性课程，要求每一位学生都自主选择一个类别的拓展性课程．为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）：

    根据统计图中的信息，解答下列问题：

    （）求本次被调查的学生人数．

    （）将条形统计图补充完整．

    （）若该校共有名学生，请估计全校选择体育类的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

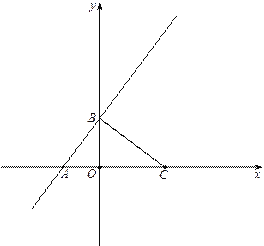
    【题目】如图，在平面直角坐标系xOy中，点C的坐标为（4，0），一次函数的图像分别交x轴、y轴于点A、点B.

    ⑴ 若点D是直线AB在第一象限内的点，且BD＝BC，试求出点D的坐标.

    ⑵ 在⑴的条件下，若点Q是坐标轴上的一个动点，试探索在第一象限是否存在另一个点P，使得以B、D、P、Q为顶点的四边形是菱形（BD为菱形的一边）？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F．

    （1）如图1，求证：AE=DF；
    （2）如图2，若AB=2，过点M作 MG⊥EF交线段BC于点G，判断△GEF的形状，并说明理由；
    （3）如图3，若AB= ，过点M作 MG⊥EF交线段BC的延长线于点G．
    ①直接写出线段AE长度的取值范围；
    ②判断△GEF的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(徐州中考)如图，在△ABC中，∠ABC＝90°，∠BAC＝60°，△ACD是等边三角形，E是AC的中点，连接BE并延长交DC于点F，求证：

    (1)△ABE≌△CFE；

    (2)四边形ABFD是平行四边形．

    查看答案和解析>>

    同步练习册答案