
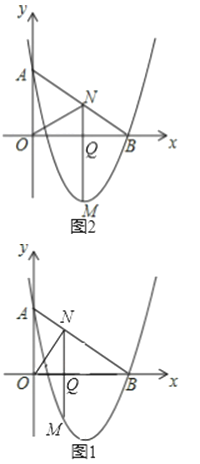
【题目】如图1,在平面直角坐标系中,O为坐标原点.直线y=kx+b与抛物线y=mx2﹣![]() x+n同时经过A(0,3)、B(4,0).
x+n同时经过A(0,3)、B(4,0).
(1)求m,n的值.
(2)点M是二次函数图象上一点,(点M在AB下方),过M作MN⊥x轴,与AB交于点N,与x轴交于点Q.求MN的最大值.
(3)在(2)的条件下,是否存在点N,使△AOB和△NOQ相似?若存在,求出N点坐标,不存在,说明理由.
【答案】解:(1)∵抛物线y=mx2﹣![]() x+n经过A(0,3)、B(4,0),
x+n经过A(0,3)、B(4,0),
∴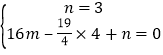 ,
,
解得![]() .
.
∴二次函数的表达式为y=x2﹣![]() x+3.
x+3.
(2)∵直线y=kx+b经过A(0,3)、B(4,0),则![]() ,
,
解得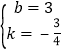 .
.
∴经过AB两点的一次函数的解析式为y=﹣![]() x+3.
x+3.
MN=﹣![]() x+3﹣(x2﹣
x+3﹣(x2﹣![]() x+3)=﹣x2+4x=﹣(x﹣2)2+4,
x+3)=﹣x2+4x=﹣(x﹣2)2+4,
∵0≤x≤4,
∴当x=2时,MN取得最大值为4.
(3)存在.
①当ON⊥AB时,(如图1)
可证:∠NOQ=∠OAB,∠OQN=∠AOB=90°,
∴△AOB∽△OQN.
∴![]()
∴OA=3,OB=4,
∴AB=5,
∵ONAB=OAOB,
∴ON=![]() ,
,
∴NQ=![]() ,OQ=
,OQ=![]() .
.
∴N(![]() ,
,![]() );
);
②当N为AB中点时,(如图2)
∠NOQ=∠B,∠AOB=∠NQO=90°,
∴△AOB∽∽△NQO.此时N(2,![]() ).
).
∴满足条件的N(![]() ,
,![]() )或N(2,
)或N(2,![]() ).
).
【解析】(1)根据抛物线y=mx2﹣![]() x+n经过A(0,3)、B(4,0),将两点坐标代入抛物线即可得出m,n的值;
x+n经过A(0,3)、B(4,0),将两点坐标代入抛物线即可得出m,n的值;
(2)根据待定系数法可求经过AB两点的一次函数的解析式,得到MN=﹣![]() x+3﹣(x2﹣
x+3﹣(x2﹣![]() x+3)=﹣x2+4x=﹣(x﹣2)2+4,从而求解;
x+3)=﹣x2+4x=﹣(x﹣2)2+4,从而求解;
(3)分两种情况讨论,①当ON⊥AB 时,②当N为AB中点时,依次求出点N的坐标即可.


科目:初中数学 来源: 题型:
【题目】从-1,1,2这三个数字中,随机抽取一个数记为a,那么,使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形的面积为![]() ,且使关于x的不等式组
,且使关于x的不等式组![]() 有解的概率为________.
有解的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD.当∠DOA=∠OBA时,直线CD的解析式为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按一定规律排列且形式相似的一列数:
第1个数:a1=![]() -(1+
-(1+![]() );
);
第2个数:a2=![]() -(1+
-(1+![]() )[1+
)[1+![]() ][1+
][1+![]() ];
];
第3个数:a3=![]() -(1+
-(1+![]() )[1+
)[1+![]() ][1+
][1+![]() ][1+
][1+![]() ](1+
](1+![]() ].
].
(1)计算这三个数的结果(直接写答案):
a1=___;a2=___;a3=___;
(2)请按上述规律写出第4个数a4的形式并计算结果;
(3)请根据上述规律写出第n (n为正整数)个数an的形式(中间部分用省略号,两端部分必须写详细),然后直接写出计算结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )
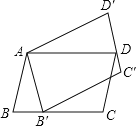
A. 100° B. 105° C. 115° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一个多边形的一个顶点与其余各顶点连接起来,可以把这个多边形分割成若干个三角形.




(1)把一个100边形的一个顶点与其余各顶点连接起来,一共可以连几条线段?
(2)在(1)中,这些线段将100边形分割成几个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图D、E、F分别在△ABC的三边上,BD=![]() AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是_________.
AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是_________.
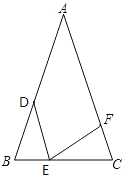
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,点A坐标为(﹣2,0),点B坐标为(0,2),点E为线段AB上的动点(点E不与点A,B重合),以E为顶点作∠OET=45°,射线ET交线段0B于点F,C为y轴正半轴上一点,且OC=AB,抛物线y=﹣ ![]() x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点. 
(1)求此抛物线的函数表达式;
(2)求证:∠BEF=∠AOE;
(3)当△EOF为等腰三角形时,求此时点E的坐标;
(4)在(3)的条件下,当直线EF交x轴于点D,P为(1)中抛物线上一动点,直线PE交x轴于点G,在直线EF上方的抛物线上是否存在一点P,使得△EPF的面积是△EDG面积的(2 ![]() +1)倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
+1)倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com