
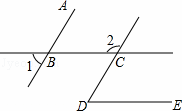
如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
考点:
平行线的判定.
分析:
由于∠1=47°,∠2=133°,则∠ABC+∠2=180°,根据平行线的判定方法得到AB∥CD;然后利用平角的定义计算出∠BCD=180°﹣133°=47°,
则∠BCD=∠D,根据平行线的判定即可得到BC∥DE.
解答:
解:BC∥DE,AB∥CD.理由如下:
∵∠1=47°,∠2=133°,
而∠ABC=∠1=47°,
∴∠ABC+∠2=180°,
∴AB∥CD;
∵∠2=133°,
∴∠BCD=180°﹣133°=47°,
而∠D=47°,
∴∠BCD=∠D,
∴BC∥DE.
点评:
本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.


科目:初中数学 来源:2012-2013学年广东江门福泉奥林匹克学校七年级下学期期中数学试卷(带解析) 题型:解答题
如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
查看答案和解析>>
科目:初中数学 来源:2015届广东江门福泉奥林匹克学校七年级下学期期中数学试卷(解析版) 题型:解答题
如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?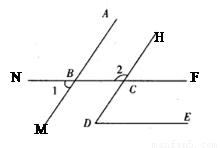
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com