练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．过m边形的顶点能作7条对角线，n边形没有对角线，k边形有k条对角线，则（m-k）n=125．

    分析 若过m边形的一个顶点有7条对角线，则m=10；n边形没有对角线，只有三角形没有对角线，因而n=3；k边形有k条对角线，即得到方程$\frac{1}{2}$k（k-3）=k，解得k=5；正h边形的内角和与外角和相等，内角和与外角和相等的只有四边形，因而h=4．代入解析式就可以求出代数式的值．

    解答 ：∵n边形从一个顶点发出的对角线有n-3条，
    ∴m=7+3=10，n=3，k=5，h=4；
    ∴（m-k）n=（10-5）3=125，
    故答案为：125．

    点评 本题考查了多边形的对角线，解决本题的关键是熟记n边形从一个顶点发出的对角线有n-3条，共有对角线$\frac{1}{2}$n（n-3）条．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    10．当y≠0时，$\frac{b}{2x}$=$\frac{by}{2xy}$，这种变形的依据是分式的基本性质．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

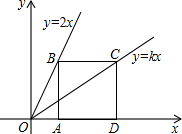    11．如图，已知四边形ABCD是正方形，点B，C分别在两条直线y=2x和y=kx上，点A，D是x轴上两点．
    （1）若此正方形边长为2，k=$\frac{2}{3}$；
    （2）若此正方形边长为a，k的值是否会发生变化？若不会发生变化说明理由；若会发生变化，试求出a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：
    （1）0.125×104×8×104
    （2）[$\frac{1}{3}$a3b5•（-15ab）+（a2b3）2]÷（2a3b3）
    （3）先化简，再求值：（-2x+1）（-2x-1）-2x（x-1），其中x=$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

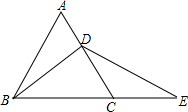    15．如图所示，△ABC为等边三角形，BD为中线，延长BC至E，使 DE=BD．
    求证：（1）CE=$\frac{1}{2}$BC．
    （2）把（1）中的BD为中线换成其它什么条件也能得到同样的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，在图中求作⊙P，使得⊙P经过点M与点N，且圆心P到∠AOB两边的距离相等（要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．先化简，再求值．已知|m-1|+（n+$\frac{1}{2}$）2=0，求（-m2n+1）（-1-m2n）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如果要使整个挂图的面积是ycm2，设金色纸边的宽为xcm，要求纸边的宽度不得少于1cm，同时不得超过2cm．
    （1）求出y关于x的函数解析式，并直接写出自变量的取值范围；
    （2）此时金色纸边的宽应为多少cm时，这幅挂图的面积最大？求出最大面积的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，一种某小区的两幢10层住宅楼间的距离为AC=30m，由地面向上依次为第1层、第2层、…、第10层，每层高度为3m．假设某一时刻甲楼在乙楼侧面的影长EC=h，太阳光线与水平线的夹角为α．
    （1）用含α的式子表示h（不必指出α的取值范围）；
    （2）当α=30°时，甲楼楼顶B点的影子落在乙楼的第几层？若α每小时增加15°，从此时起几小时后甲楼的影子刚好不影响乙楼采光？

    查看答案和解析>>

    同步练习册答案