
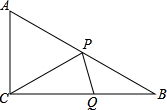
 动速度(P的速度不变),使△CPQ成为正三角形?如何改变?并求出相应的t值.
动速度(P的速度不变),使△CPQ成为正三角形?如何改变?并求出相应的t值. 解:①过P作MP⊥AC与M,作PN⊥CB于N,如图,AP=CQ=t,
解:①过P作MP⊥AC与M,作PN⊥CB于N,如图,AP=CQ=t, t,AM=
t,AM= t,
t, t,
t, t)2+(3-
t)2+(3- t)2=t2-
t)2=t2- t+9,
t+9, t,
t, t+9=(
t+9=( t)•t,整理得:t2-18t+45=0,
t)•t,整理得:t2-18t+45=0, CQ=
CQ= t,
t, t=
t= t
t CQ=
CQ= xt,
xt, xt=
xt= t,
t, ,
, t,
t, CQ,PN=CM,
CQ,PN=CM, t=
t= •
• t,
t,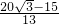 .
. cm/秒(P的速度不变),使△CPQ成为正三角形,相应的t值为
cm/秒(P的速度不变),使△CPQ成为正三角形,相应的t值为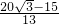 .
. t,AM=
t,AM= t,则CM=3-
t,则CM=3- t,在Rt△PCM中利用勾股定理得到PC2=PM2+MC2=(
t,在Rt△PCM中利用勾股定理得到PC2=PM2+MC2=( t)2+(3-
t)2+(3- t)2=t2-
t)2=t2- t+9;又Rt△CPN∽Rt△CQP,得到CP2=CN•CQ=
t+9;又Rt△CPN∽Rt△CQP,得到CP2=CN•CQ= t•t,由此可得到关于t的一元二次方程,解方程即可得到t的值;
t•t,由此可得到关于t的一元二次方程,解方程即可得到t的值; CQ=
CQ= t,而CN=MP,得到
t,而CN=MP,得到 t=
t= t,解得t=0不合题意;设Q的速度为x,则CQ=xt,若△CPQ为正三角形,CN=
t,解得t=0不合题意;设Q的速度为x,则CQ=xt,若△CPQ为正三角形,CN= CQ=
CQ= xt,而CN=MP=
xt,而CN=MP= t,可得到x=
t,可得到x= ,然后根据等边三角形的高为边长的
,然后根据等边三角形的高为边长的 倍得到3-
倍得到3- t=
t= •
• t,解方程求得满足条件的t的值.
t,解方程求得满足条件的t的值.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com