练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某商品原价100元，连续两次涨价x%后售价为121元，则列出的方程是_____

    【答案】100（1+x %）2=121

    【解析】第一次涨价后的价格为100×(1+x%)，

    第二次涨价后的价格为100×(1+x%)2，

    ∴可列方程为100(1+x%)2=121，

    故答案为：100（1+x %）2=121.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】用反证法证明“a＞b”时应先假设（　　）

    A.a≤bB.a＜bC.a＝bD.a≠b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一个平面内，不重合的两条直线的位置关系可能是 ( )

    A. 相交或平行 B. 相交或垂直 C. 平行或垂直 D. 不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点P的坐标为(2－a，3a＋6)，且点P到两坐标轴的距离相等，则点P的坐标是(　　)

    A. (3，3) B. (3，－3) C. (6，－6) D. (3，3)或(6，－6)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2＋bx＋c经过A（－4，3）、B（2，0）两点，当x=5和x=－5时，这条抛物线上对应点的纵坐标相等．经过点C（0，－2）的直线l与x轴平行，O为坐标原点．

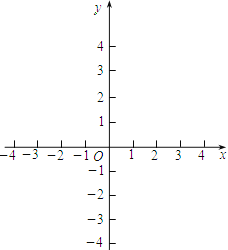
    （1）求直线AB和这条抛物线的解析式；

    （2）以A为圆心，AO为半径的圆记为⊙A，判断直线l与⊙A的位置关系，并说明理由；

    （3）设直线AB上的点D的横坐标为-1，P（m，n）是抛物线y＝ax2＋bx＋c上的动点，当△PDO的周长最小时，求四边形CODP的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点.令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α.

    （1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2=　 　°；

    （2）若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为：　 　；

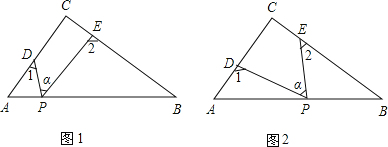
    （3）若点P运动到边AB的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由.

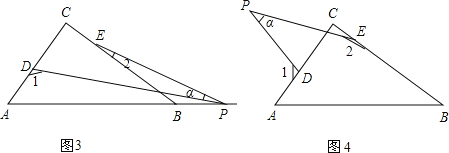
    （4）若点P运动到△ABC形外，如图（4）所示，则∠α、∠1、∠2之间的关系为：　　.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直角坐标系中，第四象限内一点P到x轴的距离为2，到y轴的距离为5，那么点P的坐标是 . 　

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点N的坐标为(a，a－1)，则点N一定不在第________象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

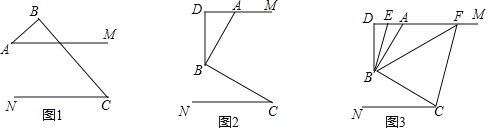
    【题目】已知AM∥CN，点B为平面内一点，AB⊥BC于B．

    （1）如图1，直接写出∠A和∠C之间的数量关系________；

    （2）如图2，过点B作BD⊥AM于点D，求证：∠ABD=∠C；

    （3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数．

    查看答案和解析>>

    同步练习册答案