
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
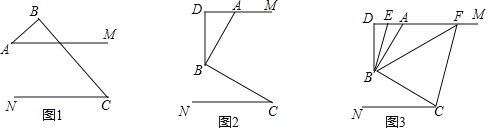
【答案】(1)∠A+∠C=90°;(2)见解析;(3)105°.
【解析】试题分析:(1)根据平行线的性质以及直角三角形的性质进行证明即可; (2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得结论;(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,设∠DBE=α,∠ABF=β,根据由∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得∠EBC=∠ABE+∠ABC=15°+90°=105°.
试题解析:
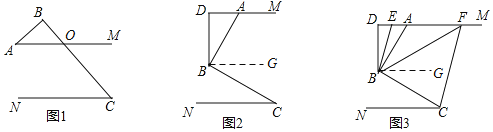
(1)如图1,∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°,
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,
∴∠C=∠CBG,
∴∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.


科目:初中数学 来源: 题型:
【题目】2017年河南省经济保持总体平稳,稳中向好发展态势,生产总值达到44988.16亿元,用科学记数法表示数据44988.16亿为( )
A. 44988.16×108 B. 4.498816×1012
C. 4.49×1012 D. 4.50×1013
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
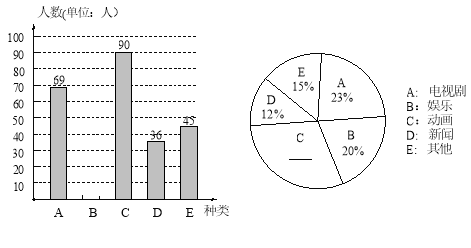
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
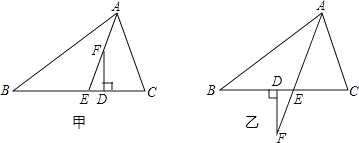
【题目】已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.
(1)试说明:∠EFD=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com