
【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.

【答案】![]()
【解析】试题分析:根据矩形性质得AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,再根据折叠性质得∠DAC=∠D′AC,而∠DAC=∠ACB,则∠D′AC=∠ACB,所以AE=EC,设BE=x,则EC=4-x,AE=4-x,然后在Rt△ABE中利用勾股定理可计算出BE.
试题解析:∵四边形ABCD为矩形,
∴AB=DC=3,BC=AD=4,AD∥BC,∠B=90,
∵△ACD沿AC折叠到△ACD′,AD′与BC交于点E,
∴∠DAC=∠D′AC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠D′AC=∠ACB,
∴AE=EC,
设BE=x,则EC=4x,AE=4x,
在Rt△ABE中,∵AB+BE=AE,
∴3+x=(4x) ,解得x=![]() ,
,
即BE的长为![]() .
.


科目:初中数学 来源: 题型:
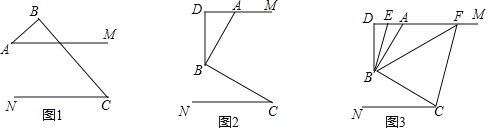
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题的是( )
A.四边形的外角和等于内角和 B.所有的矩形都相似
C.对角线相等的菱形是正方形 D.对角线互相垂直的平行四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学足球队的18名队员的年龄情况如下表:
年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
人数 | 3 | 6 | 4 | 4 | 1 |
则这些队员年龄的众数和中位数分别是( )
A.15,15 B.15,15.5 C.15,16 D.16,15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
, ![]() ,
, ![]() 三点,其中
三点,其中![]() 满足关系式
满足关系式![]() .
.
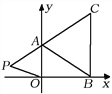
(1)求![]() 的值;
的值;
(2)如果在第二象限内有一点![]() ,那么请用含
,那么请用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(3)在(2)的条件下,是否存在点![]() ,使四边形
,使四边形![]() 的面积与三角形
的面积与三角形![]() 的面积相等?若存在,求出点
的面积相等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com