
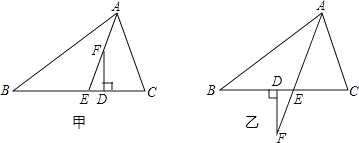
【题目】已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.
(1)试说明:∠EFD=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由.
【答案】(1) 见解析;(2) 成立,理由见解析.
【解析】试题分析:(1) 根据三角形内角和定理以及角平分线的定义得到∠BAE=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠C)=90°﹣
(180°﹣∠B﹣∠C)=90°﹣![]() (∠B+∠C),然后根据三角形的外角的性质可以得到∠FEC=∠B+∠BAE,求得∠FEC,再根据直角三角形的两个锐角互余即可求得结论;(2)根据(1)可以得到∠AEC=90°+
(∠B+∠C),然后根据三角形的外角的性质可以得到∠FEC=∠B+∠BAE,求得∠FEC,再根据直角三角形的两个锐角互余即可求得结论;(2)根据(1)可以得到∠AEC=90°+![]() (∠B﹣∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
(∠B﹣∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
试题解析:
解:(1)∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠C)
(180°﹣∠B﹣∠C)
=90°﹣![]() (∠B+∠C),
(∠B+∠C),
∵∠FEC=∠B+∠BAE,
则∠FEC=∠B+90°﹣![]() (∠B+∠C)
(∠B+∠C)
=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∵FD⊥EC,
∴∠EFD=90°﹣∠FEC,
则∠EFD=90°﹣[90°+![]() (∠B﹣∠C)]
(∠B﹣∠C)]
=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)成立.
证明:同(1)可证:∠AEC=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∴∠DEF=∠AEC=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∴∠EFD=90°﹣[90°+![]() (∠B﹣∠C)]
(∠B﹣∠C)]
=![]() (∠C﹣∠B).
(∠C﹣∠B).


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
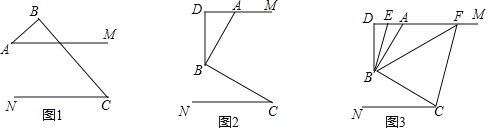
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.两条不相交的直线就是平行线
B.过任意一点可以作已知直线的一条平行线
C.过直线外任意一点作已知直线的垂线,可以作无数条
D.直线外一点与直线上各点所连接的所有线段中,垂线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:71=7,72=49,73=343,74=2401,75=16807,…那么72007+1的个位数字是( )
A. 8 B. 4 C. 2 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题的是( )
A.四边形的外角和等于内角和 B.所有的矩形都相似
C.对角线相等的菱形是正方形 D.对角线互相垂直的平行四边形是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com