
分析 (1)先将①去分母,移项,整理成成$\frac{b}{b-a}=\frac{d}{c}$,由于c与d互质,得出d=b,c=b-a;用同样的方法得出f=bd=b2,bd-ac=e即可得出结论;
(3)同(1)的方法得出g=bdf=f2,bdf-ace=511,即:f2-ace=511⑤,借助(1)得出的结论ac=f-e④,将④代入⑤得出关于e的一元二次方程,由于e,f是大于1的正整数,即可得出f=4,9,16,25,再分别用△是完全平方数排除点不符合题意的,最后利用得出的结论即可求出a,b,c,d,e,f,g.
解答 解:(1)①去分母得,bc+ad=bd,
∴bc=d(b-a),
∴$\frac{b}{b-a}=\frac{d}{c}$,
∵a与b互质,c与d互质,
∴d=b,c=b-a;
将①整体代入②得,$\frac{bd}{ac}+\frac{f}{e}=\frac{bdf}{ace}$,
去分母,移项得,bde=bdf-acf,
∴bde=f(bd-ac),
∴$\frac{bd}{bd-ac}=\frac{f}{e}$,
∵f与e互质,
∴f=bd=b2,bd-ac=e,
∴ac=bd-e=f-e④,
(2)由(1)知,ac=f-e④,
将②整体代入④得,$\frac{bdf}{ace}+\frac{g}{511}=\frac{bdfg}{511ace}$,
去分母,移项,分解得,511bdf=g(bdf-ace),
∴$\frac{bdf}{bdf-ace}=\frac{g}{511}$,
∵g与511互质,
∴g=bdf=f2,bdf-ace=511,
∴f2-ace=511⑤,
将④代入⑤化简得,e2-fe+f2-511=0,
∵e,f大于1的整数,
∴关于e的一元二次方程e2-fe+f2-511=0有实数根,
∴△=f2-4(f2-511)=2044-3f2≥0,
∴f2≤$\frac{2044}{3}$,
∵f=b2,且b,f是大于1的整数,
∴f是大于1的完全平方数,
∴f=4,9,16,25,
∵e为大于1整数,
∴△必须是完全平方数,
Ⅰ、当f=4时,△=2044-3×16=1996,而1996不是平方数,不符合题意,舍,
Ⅱ、当f=9时,△=2044-3×81=1801,而1801不是平方数,不符合题意,舍,
Ⅲ、当f=16时,△=2044-3×256=1276,而1276不是平方数,不符合题意,舍,
Ⅳ、当f=25时,△=2044-3×625=169=132,
∴g=f2=625
∵f=b2,b=d,
∴b=d=5,
∵c=b-a,
∴a+c=5,
∵a≤c,且a、c是大于1的整数,
∴a=2,c=3,
把a=2,c=3,f=25代入ac=f-e中,得e=f-ac=25-2×3=19;
即:a=2,b=5,c=3,d=5,e=19,f=25,g=625.
点评 此题主要考查了互质的意义,完全平方数,一元二次方程的整数解,一元二次方程根的判别式,解(1)的关键是得出$\frac{b}{b-a}=\frac{d}{c}$,解(2)的关键是得出e2-fe+f2-511=0;整体代入是解决此题的难点;是一道难度比较大的竞赛题.


科目:初中数学 来源: 题型:解答题
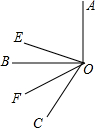 已知:如图∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
已知:如图∠BOC=60°,OE平分∠AOC,OF平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知,a,b两数在数轴上的位置如图,下列各式成立的是( )
已知,a,b两数在数轴上的位置如图,下列各式成立的是( )| A. | ab>0 | B. | (a+1)(b+1)>0 | C. | a+b>0 | D. | (a-1)(b-1)>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
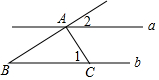 如图,已知直线a∥b,AC⊥AB,AC与直线a,b分别交于A,C两点,若∠1=60°,则∠2的度数为( )
如图,已知直线a∥b,AC⊥AB,AC与直线a,b分别交于A,C两点,若∠1=60°,则∠2的度数为( )| A. | 30° | B. | 35° | C. | 45° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)
如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 套餐 类型 | 月费 (元/月) | 套餐内包含内容 | 套餐外资费 | ||
| 国内数据流量(MB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
| 套餐1 | 18 | 100 | 0 | 0.29 元/MB | 0.19 元/分钟 |
| 套餐2 | 28 | 100 | 50 | ||
| 套餐3 | 38 | 300 | 50 | ||
| 套餐4 | 48 | 500 | 50 | ||
| A. | 套餐1 | B. | 套餐2 | C. | 套餐3 | D. | 套餐4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
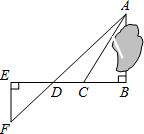 为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.根据所测数据,能出A,B间距离的有①②③(填上所有能求出A、B间距离的序号)
为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.根据所测数据,能出A,B间距离的有①②③(填上所有能求出A、B间距离的序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com