Question

5．在△ABC中，∠C=90°，AC=BC，D为BA边中点，DE⊥BC交CB于点E，G、F分别在射线DE、射线DA上，当GH经过点C时停止运动，连接FG，过F作FH⊥FG且FG=2FH，设DG=x，DF=$\sqrt{2}$x，△FHG与△ABC重合部分面积为y，y与x函数图象如图所示（0＜x≤m，m＜x≤2，2＜x≤n时解析式不同）．
（1）填空：AC=4$\sqrt{2}$．
（2）求y与x的函数关系式，并写出x的取值范围．
y=$\left\{\begin{array}{l}{\frac{5}{4}{x}^{2}}&{（0＜x≤\sqrt{2}）}\\{-\frac{5}{4}{x}^{2}-5\sqrt{2}x+5}&{（\sqrt{2}＜x≤2）}\\{-\frac{5}{12}{x}^{2}+\frac{5\sqrt{2}}{3}x+\frac{5}{3}}&{（2＜x≤\frac{7\sqrt{2}}{2}）}\end{array}\right.$．

Answer 1

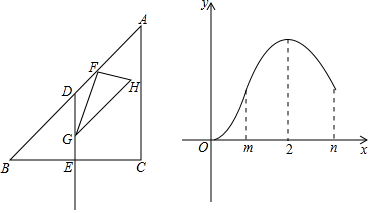
分析 （1）由题意可知当x=2时，点F与点A重合，点G与点E重合，推出AD=$\sqrt{2}$x=2$\sqrt{2}$，BD=AD=4，由CB=CA，∠ACB=90°，即可推出AC=$\frac{\sqrt{2}}{2}$AB=4．
（2）分三种情形①如图1中，当0＜x≤1时，重叠部分是△FGH．②如图2中，当1＜x≤2时，重叠部分是四边形MJFG．作FR∥EN交GH于R，HQ⊥FR于Q，交AM于W．③当2＜x≤$\frac{7}{2}$时，如图4中，重叠部分是四边形MJRW．分别求解即可．

解答 解：（1）由题意可知当x=2时，点F与点A重合，点G与点E重合，
∴AD=$\sqrt{2}$x=2$\sqrt{2}$，
∵BD=AD=2$\sqrt{2}$，CB=CA，∠ACB=90°，
∴AC=$\frac{\sqrt{2}}{2}$AB=4．
故答案为4．

（2）①如图1中，作FN⊥ED于N，HT⊥NF于T．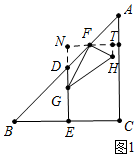

∵△DNF是等腰直角三角形，
∴DF=$\sqrt{2}$DN=$\sqrt{2}$NF，
∵DF=$\sqrt{2}$DG，
∴DG=DN=FN=x，
易知△FNG∽△HTF，
∴$\frac{FN}{TH}$=$\frac{NG}{FT}$=$\frac{FG}{FH}$=2，
∴NG=2FT，FN=2TH，
∴NF=FT=DG=x，
当点H在AC上时，NF+TF=CE=2，
∴2x=2，
∴x=1，
∴当0＜x≤1时，重叠部分是△FGH，
y=$\frac{1}{2}$•FG•FH=$\frac{1}{2}$$•\sqrt{5}$x•$\frac{\sqrt{5}}{2}$x=$\frac{5}{4}$x²．

②如图2中，当1＜x≤2时，重叠部分是四边形MJFG．作FR∥EN交GH于R，HQ⊥FR于Q，交AM于W．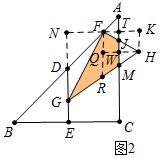

由（1）可知FN=FK，
∵FR∥GN∥KH，
∴GR=RH，
∴S_△RHF=$\frac{1}{2}$S_△FGH=$\frac{5}{8}$x²，
∵△HJM∽△HFR，
∴$\frac{{S}_{△HJM}}{{S}_{△HFR}}$=（$\frac{HW}{HQ}$）²，
∴S_△HJM=$\frac{5}{8}$x²•（$\frac{2x-2}{x}$）²=$\frac{5}{2}$x²-5x+$\frac{5}{2}$，
y=S_△FGH-S_△HJM=-$\frac{15}{8}$x²+5x-$\frac{5}{2}$．

③如图3中，当GH经过点C时，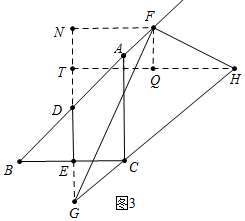

由△GEC∽△GTH，得到$\frac{EC}{TH}$=$\frac{GE}{GT}$，
∴$\frac{2}{2x}$=$\frac{x-2}{\frac{3}{2}x}$，
∴x=$\frac{7}{2}$，
∴当2＜x≤$\frac{7}{2}$时，如图4中，重叠部分是四边形MJRW．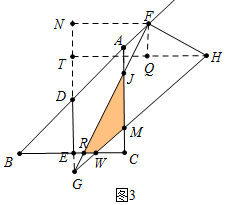

y=S_△JRC-S_△CMW=$\frac{1}{2}$•CR•CJ-$\frac{1}{2}$•CW•CM=$\frac{1}{2}$•（3-$\frac{x}{2}$）•2（3-$\frac{x}{2}$）-$\frac{1}{2}$•$\frac{14-4x}{3}$•$\frac{3}{4}$•$\frac{14-4x}{3}$=-$\frac{5}{12}$x²+$\frac{5}{3}$x+$\frac{5}{6}$．
综上所述，y=$\left\{\begin{array}{l}{\frac{5}{4}{x}^{2}}&{（0＜x≤1）}\\{\frac{5}{2}{x}^{2}-5x+\frac{5}{2}}&{（1＜x≤2）}\\{-\frac{5}{12}{x}^{2}+\frac{5}{3}x+\frac{5}{6}}&{（2＜x≤\frac{7}{2}）}\end{array}\right.$．
故答案为y=$\left\{\begin{array}{l}{\frac{5}{4}{x}^{2}}&{（0＜x≤1）}\\{\frac{5}{2}{x}^{2}-5x+\frac{5}{2}}&{（1＜x≤2）}\\{-\frac{5}{12}{x}^{2}+\frac{5}{3}x+\frac{5}{6}}&{（2＜x≤\frac{7}{2}）}\end{array}\right.$．

点评 本题考查动点问题函数图象、多边形的面积、相似三角形的判定和性质、平行线的性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加辅助线，构造相似三角形解决问题、属于中考压轴题．