
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( ) 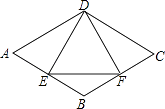
A.3
B.4
C.1
D.2
【答案】A
【解析】解:连接BD,∵四边形ABCD是菱形,
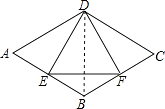
∴AD=AB,∠ADB= ![]() ∠ADC,AB∥CD,
∠ADC,AB∥CD,
∵∠A=60°,
∴∠ADC=120°,∠ADB=60°,
同理:∠DBF=60°,
即∠A=∠DBF,
∴△ABD是等边三角形,
∴AD=BD,
∵∠ADE+∠BDE=60°,∠BDE+∠BDF=∠EDF=60°,
∴∠ADE=∠BDF,
∵在△ADE和△BDF中,
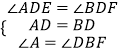 ,
,
∴△ADE≌△BDF(ASA),
∴DE=DF,AE=BF,故①正确;
∵∠EDF=60°,
∴△EDF是等边三角形,
∴②正确;
∴∠DEF=60°,
∴∠AED+∠BEF=120°,
∵∠AED+∠ADE=180°﹣∠A=120°,
∴∠ADE=∠BEF;
故④正确.
∵△ADE≌△BDF,
∴AE=BF,
同理:BE=CF,
但BE不一定等于BF.
故③错误.
综上所述,结论正确的是①②④.
故选:A.
【考点精析】利用等腰三角形的判定和菱形的性质对题目进行判断即可得到答案,需要熟知如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s). 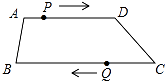
(1)用含t的代数式表示: AP=;DP=;BQ=;CQ= .
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一场篮球赛中,球员甲跳起投篮,已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,当球水平运行4 m时达到离地面的最大高度4 m.设篮球运行的轨迹为抛物线的一部分,篮圈距地面3 m,在篮球比赛中,当进攻方球员要投篮时,防守方球员常借身高优势及较强的弹跳封杀对方,这就是平常说的盖帽.(注:盖帽应在球达到最高点前进行,否则就是“干扰球”,属犯规.)
m,与篮圈中心的水平距离为7 m,当球水平运行4 m时达到离地面的最大高度4 m.设篮球运行的轨迹为抛物线的一部分,篮圈距地面3 m,在篮球比赛中,当进攻方球员要投篮时,防守方球员常借身高优势及较强的弹跳封杀对方,这就是平常说的盖帽.(注:盖帽应在球达到最高点前进行,否则就是“干扰球”,属犯规.)
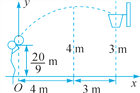
(1)问:此球能否投中?
(2)此时,防守方球员乙前来盖帽,已知乙的最大摸球高度为3.19 m,则他如何做才能成功?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】月球的半径约为1738000m,1738000这个数用科学记数法可表示为( )
A.1.738×106
B.1.738×107
C.0.1738×107
D.17.38×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
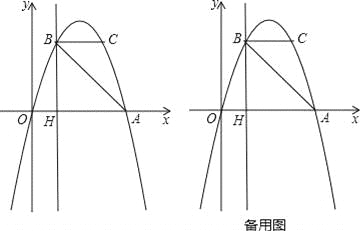
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
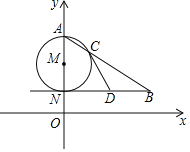
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com