
ĄŸÌâÄżĄżÒŃÖȘÊęÖáÉÏAŁŹBÁœ”ă¶ÔÓŠ”ÄÊę·Ö±đÎȘaŁŹbŁŹÇÒaŁŹbÂúŚă|a+20|=©Łšb©13Ł©2ŁŹ”ăC¶ÔÓŠ”ÄÊęÎȘ16ŁŹ”ăD¶ÔÓŠ”ÄÊęÎȘ©13Łź
Łš1Ł©ÇóaŁŹb”ÄÖ”Ł»
Łš2Ł©”ăAŁŹBŃŰÊęÖáÍŹÊ±łö·ąÏàÏòÔÈËÙÔ˶ŻŁŹ”ăA”ÄËÙ¶ÈÎȘ6žö”„λ/Ă룏”ăB”ÄËÙ¶ÈÎȘ2žö”„λ/Ă룏ÈôtĂëʱ”ăA”œÔ”ă”ÄŸàÀëșÍ”ăB”œÔ”ă”ÄŸàÀëÏà”ÈŁŹÇót”ÄÖ”Ł»
Łš3Ł©ÔÚŁš2Ł©”ÄÌőŒțÏÂŁŹ”ăAŁŹBŽÓÆđʌλÖĂÍŹÊ±łö·ąŁź”±A”ăÔ˶Ż”œ”ăCʱŁŹŃžËÙÒÔÔÀŽ”ÄËٶȷ”»ŰŁŹ”œŽïłö·ą”ășóŁŹÓÖŐÛ·”Ïò”ăCÔ˶ŻŁźB”ăÔ˶ŻÖÁD”ășóÍŁÖčÔ˶ŻŁŹ”±BÍŁÖčÔ˶ŻÊ±”ăAÒČÍŁÖčÔ˶ŻŁźÇóÔÚŽËčęłÌÖĐŁŹAŁŹBÁœ”ăÍŹÊ±”œŽï”Ä”ăÔÚÊęÖáÉ϶ÔÓŠ”ÄÊ꣟
ĄŸŽđ°žĄżŁš1Ł©a=©20ŁŹc=13Ł»Łš2Ł©t”ÄÖ”ÎȘ![]() s»ò
s»ò ![]() sŁźŁš3Ł©
sŁźŁš3Ł©![]() ŁŹ©
ŁŹ©![]() Łź
Łź
ĄŸœâÎöĄżÊÔÌâ·ÖÎöŁșŁš1Ł©žùŸĘ·ÇžșÊę”ÄĐÔÖÊŁŹœšÁą·œłÌÇółöaŁŹb”ÄÖ”Ł»
Łš2Ł©žùŸĘAŁŹBÁœ”ă”œÔ”ăO”ÄŸàÀëÏà”È·ÖÁœÖÖÇéżöŁŹ”±AĄąBÔÚÔ”ă”ÄÓÒČàAĄąBÏàÓöșÍAĄąBÔÚÔ”ă”ÄÒìČàʱŁŹœšÁą·œłÌÇółöÆäœâŒŽżÉŁ»
Łš3Ł©·ÖÈęÖÖÇéżöÌÖÂÛŁș”±AĄąBÔÚÔ”ă”ÄÓÒČàÏàÓöʱŁ»”±”ăAŽÓ”ăC·”»Űłö·ą”ăʱÓëBÏàÓöŁ»”±”ăAŽÓłö·ą”ă·”»Ű”ăCʱÓë”ăBÏàÓöŁź·Ö±đÒÀŸĘÏ߶ΔÄșÍČîčŰÏ”ÁĐ·œłÌÇóœâŒŽżÉŁź
ÊÔÌâœâÎöŁșœâŁșŁš1Ł©ÓÉÌâÒâ”ĂŁș|a+20|+Łšb©13Ł©2=0ŁŹĄàa+20=0ŁŹb©13=0ŁŹœâ”ĂŁșa=©20ŁŹc=13Ł»
Łš2Ł©Ąß”ăB¶ÔÓŠ”ÄÊęÎȘ13ŁŹA¶ÔÓŠ”ÄÊęÊÇ©20ŁŹĄàAB=36ŁŹAO=20ŁŹBO=13Łź
”±AĄąBÔÚÔ”ă”ÄÒìČàʱŁŹÈô”ăA”œÔ”ă”ÄŸàÀëșÍ”ăB”œÔ”ă”ÄŸàÀëÏà”ÈŁŹÔò
ĄĄ20©6t=13©2tŁŹœâ”ĂŁșt=![]() Łź
Łź
”±AĄąBÔÚÔ”ă”ÄÓÒČàÏàÓöʱŁŹ”ăA”œÔ”ă”ÄŸàÀëșÍ”ăB”œÔ”ă”ÄŸàÀëÏà”ÈŁŹÔò
6t+2t=33ŁŹt=![]() ŁŹĄàAŁŹBÁœ”ă”œÔ”ăO”ÄŸàÀëÏà”ÈʱŁŹt”ÄÖ”ÎȘ
ŁŹĄàAŁŹBÁœ”ă”œÔ”ăO”ÄŸàÀëÏà”ÈʱŁŹt”ÄÖ”ÎȘ![]() s»ò
s»ò ![]() sŁź
sŁź
Łš3Ł©B”ăÔ˶ŻÖÁD”ăËùĐè”ÄʱŒäÎȘ26ĄÂ2=13ŁšsŁ©ŁŹčÊtĄÜ13Łź
ÓÉŁš2Ł©”ĂŁŹ”±t=![]() ʱŁŹAŁŹBÁœ”ăÍŹÊ±”œŽï”Ä”ă±íÊŸ”ÄÊęÊÇ13©
ʱŁŹAŁŹBÁœ”ăÍŹÊ±”œŽï”Ä”ă±íÊŸ”ÄÊęÊÇ13©![]() ĄÁ2=
ĄÁ2=![]() Ł»
Ł»
ÓÉÌâÒâ”ĂŁș”±”ăAŽÓ”ăC·”»Űłö·ą”ăʱŁŹÈôÓëBÏàÓöŁŹÔò
6t©2t=20+16+Łš16©13Ł©ŁŹœâ”ĂŁșt=![]() ŁŹŽËʱAŁŹBÁœ”ăÍŹÊ±”œŽï”Ä”ă±íÊŸ”ÄÊęÊÇ13©
ŁŹŽËʱAŁŹBÁœ”ăÍŹÊ±”œŽï”Ä”ă±íÊŸ”ÄÊęÊÇ13©![]() ĄÁ2=©
ĄÁ2=©![]() Łź
Łź
”±”ăAŽÓłö·ą”ă·”»Ű”ăCʱŁŹÈôÓë”ăBÏàÓöŁŹÔò
6t+2t=2Łš20+16Ł©+20+13ŁŹœâ”Ăt=13![]() ŁšČ»șÏÌâÒ⣩Ł»
ŁšČ»șÏÌâÒ⣩Ł»
ŚÛÉÏËùÊöŁșAŁŹBÁœ”ăÍŹÊ±”œŽï”Ä”ăÔÚÊęÖáÉϱíÊŸ”ÄÊęÎȘŁș ![]() ŁŹ©
ŁŹ©![]() Łź
Łź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘĄőABCDÖĐŁŹDEÊÇĄÏADC”ÄœÇÆœ·ÖÏߣŹœ»BCÓÚ”ăEŁź
Łš1Ł©ÇóÖ€ŁșCD=CEŁ»
Łš2Ł©ÈôBE=CEŁŹÇóÖ€ŁșAEĄÍDE.

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż18ÊÀŒÍŚîœÜłö”ÄÈđÊżÊęѧŒÒĆ·ÀŁŹŚîÏÈ°ŃčŰÓÚx”ĶàÏîÊœÓĂ·ûșĆĄ°fŁšxŁ©Ą±±íÊŸŁŹÈçfŁšxŁ©Łœ©3x2+2x©1ŁŹ°ŃxŁœ©2ʱ¶àÏîÊœ”ÄÖ”±íÊŸÎȘfŁš©2Ł©ŁŹÔòfŁš©2Ł©Łœ_____Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŽÓÈ„Äê·ąÉú·ÇÖȚÖíÎÁÒÔÀŽŁŹžś”ŰÖíÈâœôȱŁŹŒÛžńÒ»ÔÙìÉ꣏ÎȘÆœÎÈÈâŒÛŁŹÄłÎïÁśč«ËŸÊÜĂüœ«300¶ÖÖíÈâÔËÍùÄł”ŰŁŹÏÖÓĐAŁŹBÁœÖÖĐÍșƔij”čČ19ÁŸżÉč©”śÓĂŁŹÒŃÖȘAĐÍł”ĂżÁŸżÉŚ°20¶ÖŁŹBĐÍł”ĂżÁŸżÉŚ°15¶ÖŁźÔÚČ»łŹÔŰ”ÄÌőŒțÏÂŁŹ19ÁŸł”ÇĄșĂ°Ń300¶ÖÖíÈâÒ»ŽÎÔËÍêŁŹÔòĐèAŁŹBĐÍł”žś¶àÉÙÁŸŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒÔÏÂÁĐžśŚéÏ߶γ€ÎȘ±ßŁŹČ»ÄÜŚéłÉÈęœÇĐΔÄÊÇ( )
A.8Ąą7Ąą13B.3Ąą4Ąą12C.5Ąą5Ąą3D.5Ąą7Ąą11
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹĆŚÎïÏß![]() ŸčęBŁš©1ŁŹ0Ł©ŁŹDŁš©2ŁŹ5Ł©Áœ”㣏ÓëxÖáÁíÒ»œ»”ăÎȘAŁŹ”ăHÊÇÏ߶ÎABÉÏÒ»¶Ż”㣏čę”ăH”ÄÖ±ÏßPQĄÍxÖᣏ·Ö±đœ»Ö±ÏßADĄąĆŚÎïÏßÓÚ”ăQŁŹPŁź
ŸčęBŁš©1ŁŹ0Ł©ŁŹDŁš©2ŁŹ5Ł©Áœ”㣏ÓëxÖáÁíÒ»œ»”ăÎȘAŁŹ”ăHÊÇÏ߶ÎABÉÏÒ»¶Ż”㣏čę”ăH”ÄÖ±ÏßPQĄÍxÖᣏ·Ö±đœ»Ö±ÏßADĄąĆŚÎïÏßÓÚ”ăQŁŹPŁź
Łš1Ł©ÇóĆŚÎïÏߔĜâÎöÊœŁ»
Łš2Ł©ÊÇ·ńŽæÔÚ”ăPŁŹÊčĄÏAPB=90ĄăŁŹÈôŽæÔÚŁŹÇółö”ăP”ÄșáŚű±êŁŹÈôČ»ŽæÔÚŁŹË”ĂśÀíÓÉŁ»
Łš3Ł©ÁŹœÓBQŁŹÒ»¶Ż”ăMŽÓ”ăBłö·ąŁŹŃŰÏ߶ÎBQÒÔĂżĂë1žö”„λ”ÄËÙ¶ÈÔ˶Ż”œQŁŹÔÙŃŰÏ߶ÎQDÒÔĂżĂë![]() žö”„λ”ÄËÙ¶ÈÔ˶Ż”œDșóÍŁÖ裏”±”ăQ”ÄŚű±êÊǶàÉÙʱŁŹ”ăMÔÚŐûžöÔ˶ŻčęłÌÖĐÓĂʱtŚîÉÙŁż
žö”„λ”ÄËÙ¶ÈÔ˶Ż”œDșóÍŁÖ裏”±”ăQ”ÄŚű±êÊǶàÉÙʱŁŹ”ăMÔÚŐûžöÔ˶ŻčęłÌÖĐÓĂʱtŚîÉÙŁż

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚÒ»Ìő±ÊÖ±”Äč«Â·ÉÏÓĐ![]() Ąą
Ąą![]() Áœ”ŰŁŹŒŚŽÓ
Áœ”ŰŁŹŒŚŽÓ![]() ”ŰÈ„
”ŰÈ„![]() ”ŰŁŹÒÒŽÓ
”ŰŁŹÒÒŽÓ![]() ”ŰÈ„
”ŰÈ„![]() ”ŰÈ»șóÁąŒŽÔ··”»Ű
”ŰÈ»șóÁąŒŽÔ··”»Ű![]() ”ŰŁŹ·”»Űʱ”ÄËÙ¶ÈÊÇÔÀŽ”Ä2±¶ŁŹÈçÍŒÊÇŒŚĄąÒÒÁœÈËÀë
”ŰŁŹ·”»Űʱ”ÄËÙ¶ÈÊÇÔÀŽ”Ä2±¶ŁŹÈçÍŒÊÇŒŚĄąÒÒÁœÈËÀë![]() ”Ű”ÄŸàÀë
”Ű”ÄŸàÀë![]() ŁšÇ§ĂŚŁ©șÍʱŒä
ŁšÇ§ĂŚŁ©șÍʱŒä![]() ŁšĐĄÊ±Ł©ÖźŒä”ÄșŻÊęÍŒÏóŁź
ŁšĐĄÊ±Ł©ÖźŒä”ÄșŻÊęÍŒÏóŁź
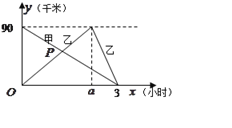
ÇëžùŸĘÍŒÏó»ŰŽđÏÂÁĐÎÊÌâŁș
Łš1Ł©![]() Ąą
Ąą![]() Áœ”Ű”ÄŸàÀëÊÇ Ç§ĂŚŁŹ
Áœ”Ű”ÄŸàÀëÊÇ Ç§ĂŚŁŹ ![]() Ł»
Ł»
Łš2Ł©Çó![]() ”ÄŚű±êŁŹČąœâÊÍËü”ÄÊ”ŒÊÒâÒ棻
”ÄŚű±êŁŹČąœâÊÍËü”ÄÊ”ŒÊÒâÒ棻
Łš3Ł©ÇëÖ±œÓĐŽłö”±![]() ÈĄșÎ֔ʱŁŹŒŚÒÒÁœÈËÏàŸà15ǧÌŁź
ÈĄșÎ֔ʱŁŹŒŚÒÒÁœÈËÏàŸà15ǧÌŁź
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com