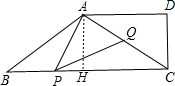
解:(1)作AH⊥BC,垂足为H.
由∠D=90°,得 DC⊥AD,
由AD∥BC,得 DC⊥BC.
又∵AH⊥BC,
∴AH=DC=6.
在Rt△ABH中,sinB=
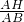
,
∵sinB=

,AH=6,
∴AB=10;
由勾股定理得 BH=8.
由AD∥BC,得∠DAC=∠ACB,
又∵∠DAC=∠B,
∴∠ACB=∠B,
∴AB=AC.
又∵AH⊥BC,
∴BC=2BH=16.
(2)∵∠APC=∠B+∠BAP=∠APQ+∠QPC,
又∵∠APQ=∠B,
∴∠BAP=∠QPC,
又∵∠B=∠ACB,即∠B=∠QCP,
∴△ABP∽△PCQ.
∴
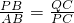
,
即
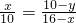
.
整理得
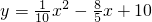
,
(0<x<16).
(3)当△APQ是等腰三角形时,分三种情况:
①当PA=PQ时,
∵∠B=∠QCP,∠BAP=∠QPC,∴△ABP≌△PCQ;
∴PC=AB,即BC-PB=AB,
∴16-x=10,解得 x=6;
②当AQ=PQ时,∠QAP=∠APQ,
∵∠APQ=∠B,∴∠QAP=∠B,即∠PAC=∠B;
又∵∠ACP=∠BCA(公共角),∴△ACP∽△BCA;
∴
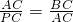
,
∴AC
2=PC•BC,即10
2=(16-x)•16,
解得
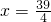
;
③当AQ=AP时,则有∠AQP=∠APQ,
∵∠APQ=∠ACB,∴∠AQP=∠ACB,
此时,点Q与点C重合,则有点P与点B重合,这与点P不与点B重合矛盾,所以AQ≠AP;
综上所述,当△APQ是等腰三角形时,x=6或
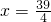
.
分析:(1)过A作AH⊥BC于H,已知∠DAC=∠B,易知∠DAC=∠BCA,则∠B=∠ACB,△ABC是等腰三角形,根据等腰三角形三线合一的性质知BC=2BH,因此欲求BC,只需求得BH即可;Rt△ABH中,已知了AH(即CD)的长和∠B的正弦值,通过解直角三角形即可求得BH的长,由此得解;
(2)此题可通过证△ABP∽△PQC,根据得到的比例线段来求出x、y的函数关系式;
(3)此题要分三种情况讨论:
①AP=PQ,此时(2)中得到的两个相似三角形应该全等,得PC=AB=AC,由此可求得x的值;
②AQ=PQ,此时∠PAQ=∠APQ=∠B,易证得△BCA∽△ACP,根据得到的比例线段可求得x的值;
③AP=AQ,此时∠APQ=∠AQP,而∠APQ=∠B=∠ACB,即∠AQP=∠ACP,那么Q、C重合,P、B重合,与已知不相符,此种情况不成立.
综合上述三种情况即可得到符合条件的x的值.
点评:此题考查了梯形的性质、相似三角形与全等三角形的判定和性质以及等腰三角形的判定和性质等知识,同时还考查了分类讨论的数学思想.

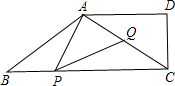 如图,在梯形ABCD中,AD∥BC,∠D=90°,DC=6,sinB=
如图,在梯形ABCD中,AD∥BC,∠D=90°,DC=6,sinB= ,点P、Q分别是边BC、对角线AC上的动点,(点P不与B、C重合),∠APQ=∠DAC=∠B,设PB=x,AQ=y.
,点P、Q分别是边BC、对角线AC上的动点,(点P不与B、C重合),∠APQ=∠DAC=∠B,设PB=x,AQ=y. 解:(1)作AH⊥BC,垂足为H.
解:(1)作AH⊥BC,垂足为H.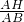 ,
, ,AH=6,
,AH=6,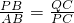 ,
,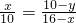 .
.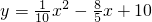 ,
,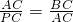 ,
,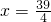 ;
; 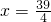 .
. 

 阅读快车系列答案
阅读快车系列答案 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )