Question

将一副三角板如图1摆放．∠AOB=60°，∠COD=45°，OM平分AOD，ON平分∠COB．
（1）∠MON=______；
（2）将图1中的三角板OCD绕点D旋转到图2的位置，求∠MON；
（3）将图1中的三角板OCD绕点D旋转到图3的位置，求∠MON．

Answer 1

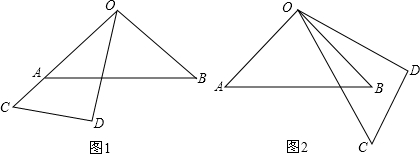
解：（1）∵∠AOB=60°，OM平分AOD，
∴∠MOB=30°，
∵∠COD=45°，ON平分∠COB，
∴∠BON=22.5°，
∴∠MON=∠MOB+∠BON=30°+22.5°=52.5°．
故答案为：52.5°．

（2）设∠AOM=∠DOM=x，∠CON=∠BON=y，则∠BOD=60-x，
∵∠COD=45゜，
∴60-2x+2y=45゜，x-y=75°，
∴∠MON=x+（60-2x）+y=60-（x-y）=52.5°．

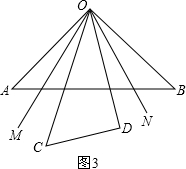
（3）设∠AOM=x=∠DOM，则∠BOM=60-x，
∵∠BOD=∠DOM-∠BOM，
∴∠BOD=x-（60-x）=2x-60，
∵∠COB=∠BOD+∠DOC，
∴∠COB=（2x-60）+45=2x-15，
∴∠CON=∠BON=（2x-15）=x-7.5，
∴∠MON=∠BOM+∠BON=60-x+x-7.5=52.5°．
分析：（1）根据∠AOB=60°，OM平分AOD和∠COD=45°，ON平分∠COB，分别求出∠MOB和∠BON的度数，再根据∠MON=∠MOB+∠BON，即可得出答案；
（2）先设∠AOM=∠DOM=x，∠CON=∠BON=y，则∠BOD=60-x，根据∠AOB=60°，∠COD=45°，列出算式，求出x-y的度数，最后根据∠MON与各角之间的关系，即可求出答案；
（3）先设∠AOM=x=∠DOM，则∠BOM=60-x，根据∠BOD=∠DOM-∠BOM，得出∠BOD的度数，再根据∠COB=∠BOD+∠DOC，求出∠CON=∠BON，最后根据∠MON=∠BOM+∠BON，即可得出答案．
点评：此题考查了角的计算，仔细体会设一个未知数（或两个未知数），用代数方法解决几何问题是本题的关键．