
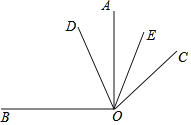
【题目】如图,已知在同一平面内OA⊥OB,OC是OA绕点O顺时针方向旋转α(α<90°)度得到,OD平分∠BOC,OE平分∠AOC.
(1)若α=60即∠AOC=60°时,求∠BOC,∠DOE.
(2)在α的变化过程中,∠DOE的度数是一个定值吗?若是定值,请求出这个值;若不是定值,请说明理由.
【答案】(1)150°;45°;(2)∠DOE的度数是一个定值.理由见解析.
【解析】
(1)先得到∠BOC=∠AOB+∠AOC=150°,再根据角平分线的定义得到∠DOC=75°,∠EOC=30°,然后计算∠DOC-∠EOC得到∠DOE的度数;
(2)根据角平分线的定义∠DOC=![]() ∠BOC=45°+
∠BOC=45°+![]() α,∠EOC=
α,∠EOC=![]() ∠AOC=
∠AOC=![]() α,所以∠DOE=∠DOC-∠EOC=45°,从而可判断∠DOE的度数是一个定值.
α,所以∠DOE=∠DOC-∠EOC=45°,从而可判断∠DOE的度数是一个定值.
解:(1)∵OA⊥OB,
∴∠AOB=90°,
∴∠BOC=∠AOB+∠AOC=90°+60°=150°,
∵OD平分∠BOC,
∴∠DOC=![]() ∠BOC=75°,
∠BOC=75°,
∵OE平分∠AOC,
∴∠EOC=![]() ∠AOC=30°,
∠AOC=30°,
∴∠DOE=∠DOC-∠EOC=75°-30°=45°;
(2)在α的变化过程中,∠DOE的度数是一个定值,为45°.
∵OD平分∠BOC,
∴∠DOC=![]() ∠BOC=
∠BOC=![]() (90°+α)=45°+
(90°+α)=45°+![]() α
α
∵OE平分∠AOC,
∴∠EOC=![]() ∠AOC=
∠AOC=![]() α,
α,
∴∠DOE=∠DOC-∠EOC=45°+![]() α-
α-![]() α=45°,
α=45°,
即∠DOE的度数是一个定值.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
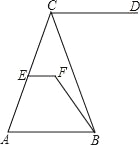
【题目】如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系?加以证明;
(2)若∠CEF=70°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2)
(1)连接A、B、C三点,请在如图中作出△ABC关于x轴对称的图形△A’B’C’并直接写出各对称点的坐标;(2)求△ABC的面积;(3)若M(x,y)是△ABC内部任意一点,请直接写出点M在△A’B’C’内部的对应点M1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小兰和小潭分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小兰掷得的点数为x,小谭掷得的点数为y,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为()
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别写有数字-1,1,2的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,小明要与父母外出游玩,带了2件上衣和3条长裤(把衣服和裤子分别装在两个袋子里),上衣颜色有红色、黄色,长裤有红色、黑色、黄色.
问题为:
(1)小明随意拿出一条裤子和一件上衣配成一套,用(画树状图或列表格)中的一种列出所有可能出现结果;
(2)配好一套衣服,小明正好拿到黑色长裤的概率是多少;
(3)他任意拿出一件上衣和一条长裤穿上的颜色正好相同的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
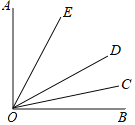
【题目】如图,已知∠AOB内部有三条射线,OE平分∠AOD,OC平分∠BOD.
(1)若∠AOB=90°,求∠EOC的度数;
(2)若∠AOB=α,求∠EOC的度数;
(3)如果将题中“平分”的条件改为∠EOA=![]() ∠AOD,∠DOC=
∠AOD,∠DOC=![]() ∠DOB,∠AOD=50°,且∠AOB=90°,求∠EOC的度数.
∠DOB,∠AOD=50°,且∠AOB=90°,求∠EOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
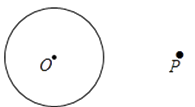
小敏的作法如下:
如图,
①链接op,做线段op的垂直平分线MN,交OP于点C
②以点C为圆心,CO的长为半径作圆,交⊙O于A、B两点
③作直线PA、PB所以直线PA,PB就是所求的切线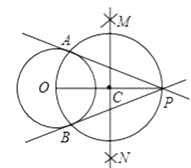
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E. F.

(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com