Question

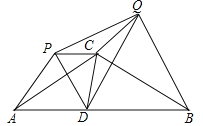
【题目】如图，等腰△ABC中，CA=CB=4，∠ACB=120°，点D在线段AB上运动（不与A、B重合），将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，给出下列结论：

①CD=CP=CQ；

②∠PCQ的大小不变；

③△PCQ面积的最小值为；

④当点D在AB的中点时，△PDQ是等边三角形，其中所有正确结论的序号是 ．

Answer 1

【答案】①②④．

【解析】

试题分析：①∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，∴CP=CD=CQ，∴①正确；

②∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，∴∠ACP=∠ACD，∠BCQ=∠BCD，∴∠ACP+∠BCQ=∠ACD+∠BCD=∠ACB=120°，∴∠PCQ=360°﹣（∠ACP+BCQ+∠ACB）=360°﹣（120°+120°）=120°，∴∠PCQ的大小不变；∴②正确；

③如图，过点Q作QE⊥PC交PC延长线于E，∵∠PCQ=120°，∴∠QCE=60°，在Rt△QCE中，tan∠QCE=，∴QE=CQ×tan∠QCE=CQ×tan60°=CQ，∵CP=CD=CQ，∴S△PCQ=CP×QE=CP×CQ=，∴CD最短时，S△PCQ最小，即：CD⊥AB时，CD最短，过点C作CF⊥AB，此时CF就是最短的CD，∵AC=BC=4，∠ACB=120°，∴∠ABC=30°，∴CF=BC=2，即：CD最短为2，∴S△PCQ最小===，∴③错误；

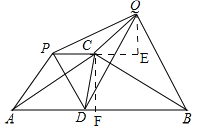
④∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，∴AD=AP，∠DAC=∠PAC，∵∠DAC=30°，∴∠APD=60°，∴△APD是等边三角形，∴PD=AD，∠ADP=60°，同理：△BDQ是等边三角形，∴DQ=BD，∠BDQ=60°，∴∠PDQ=60°，∵当点D在AB的中点，∴AD=BD，∴PD=DQ，∴△DPQ是等边三角形，∴④正确，故答案为：①②④．