
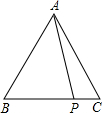
 如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,求AP2+PB•BC的值.
如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,求AP2+PB•BC的值. 分析 首先过点A作AD⊥BC于D,可得∠ADP=∠ADB=90°,又由AB=AC,根据三线合一的性质,可得BD=CD,由勾股定理可得PA2=PD2+AD2,AD2+BD2=AB2,然后由AP2+PB•PC=AP2+(BD+PD)(CD-PD),即可求得答案.
解答 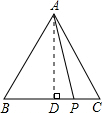 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D,
∵AB=AC=5,∠ADP=∠ADB=90°,
∴BD=CD,PA2=PD2+AD2,AD2+BD2=AB2,
∴AP2+PB•PC=AP2+(BD+PD)(CD-PD)=AP2+(BD+PD)(BD-PD)=AP2+BD2-PD2=AP2-PD2+BD2=AD2+BD2=AB2=25.
即AP2+PB•BC=25.
点评 本题考查了勾股定理与等腰三角形的性质的正确及灵活运用.注意得到AP2+PB•PC=AP2+(BD+PD)(CD-PD)是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 75cm,115cm | B. | 60cm,100cm | C. | 85cm,125cm | D. | 45cm,85cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 道二进行学校规划,工程师需测某教学楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得教学楼顶端A的仰角为60°,教学楼AB的高时多少?
道二进行学校规划,工程师需测某教学楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得教学楼顶端A的仰角为60°,教学楼AB的高时多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
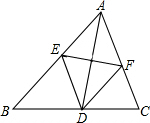 如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB、AC于点E、F.
如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB、AC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com