
分析 首先化简$\frac{{x}^{2}-6x+9}{{x}^{2}-9}$÷$\frac{x-3}{2}$,然后把x=-2代入化简后的算式,求出算式的值是多少即可.
解答 解:$\frac{{x}^{2}-6x+9}{{x}^{2}-9}$÷$\frac{x-3}{2}$
=$\frac{{(x-3)}^{2}}{(x-3)(x+3)}$•$\frac{2}{x-3}$
=$\frac{2}{x+3}$
当x=-2时,
原式=$\frac{2}{-2+3}$=2
点评 此题主要考查了分式的化简求值问题,要熟练掌握,化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
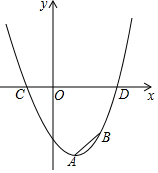 二次函数y=x2-2x-c 的图象如图所示,A,B两点的纵坐标分别为-4,-3,且AB=$\sqrt{2}$.
二次函数y=x2-2x-c 的图象如图所示,A,B两点的纵坐标分别为-4,-3,且AB=$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
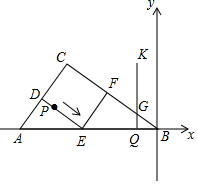 如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.以AB所在直线为x轴,B点为坐标原点建立平面直角坐标系,点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长度的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长度的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G,点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.以AB所在直线为x轴,B点为坐标原点建立平面直角坐标系,点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长度的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长度的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G,点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
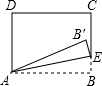 如图,矩形ABCD中,点E为射线BC上的一个动点,连接AE,以AE为对称轴折叠△AEB,得到△AEB′,点B的对称点为点B′,若AB=5,BC=3,当点B′落在射线CD上时,线段BE的长为$\frac{5}{3}$或15.
如图,矩形ABCD中,点E为射线BC上的一个动点,连接AE,以AE为对称轴折叠△AEB,得到△AEB′,点B的对称点为点B′,若AB=5,BC=3,当点B′落在射线CD上时,线段BE的长为$\frac{5}{3}$或15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com