
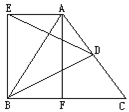
【题目】已知,如图,等边△ABC中,AD=DC,BF=FC,△BDE是等边三角形.求证:四边形AEBF是矩形.
【答案】见解析
【解析】
根据等边三角形的性质可得AF=BD=BE,再求出∠EBF=∠AFB=90°,连接EF,然后利用“边角边”证明△ABF和△EFB全等,根据全等三角形对应边相等可得AB=EF,再证出四边形AEBF是平行四边形,然后根据对角线相等的平行四边形是矩形证明即可.
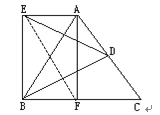
证明:连接EF,
∵等边△ABC中,点D是AC的中点,F是BC的中点,
∴AF=BD,∠CBD=30°,∠AFB=90°
∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠EBF=∠DBE+∠CBD=90°
∴AF=BD=BE,∠EBF=∠AFB,
在△ABF和△EFB中,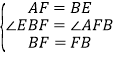
∴△ABF≌△EFB(SAS),
∴AB=EF,
∵∠AFB=∠EBF=90°,
∴AF∥BE,
又∵AF=BE,
∴四边形AEBF是平行四边形,
∵AB=EF,
∴四边形AEBF是矩形,
故AB=EF,且四边形AEBF是矩形.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写下表:
图形序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子个数 | 5 | 8 | … |
(2)写出第n个“T”字形图案中棋子的个数_________________(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子____________个?
(4)计算前20个“T”字形图案中棋子的总个数.
(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你填空:
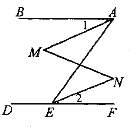
解:∵∠BAE+∠AED=180° (已知) ,
∴AB//DE( ),
∴∠BAE= ( )
又 ∵∠1=∠2(已知)
∴∠BAE-∠1= - (等式性质),
即∠MAE=∠NEA,
∴ ∥ ( ),
∴∠M=∠N(两直线平行,内错角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为线段AB上一点,AB=6,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)若AO=4,
①当t=1秒时,OP= , S△ABP=;
②当△ABP是直角三角形时,求t的值;
(2)如图2,若点O为AB中点,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求AQBP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)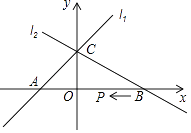
(1)求a、b的值;
(2)过动点Q(n,0)且垂直于x轴的直线与l1、l2分别交于点M、N都位于x轴上方时,求n的取值范围;
(3)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题.
(1)不改变分式的值,把下列分子和分母的最高次的系数都化为正数![]() ________.
________.
(2)不改变分式的值,把下列分子和分母的中各项系数都化为整数![]() ________.
________.
(3)若分式![]() 的值是整数,求整数
的值是整数,求整数![]() 的值.
的值.
(4)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
(1)若AC=9cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,点B2013的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,点B2013的坐标为( )

A. (42012×![]() ,42012) B. (24026×
,42012) B. (24026×![]() ,24026) C. (24026×
,24026) C. (24026×![]() ,24024) D. (44024×
,24024) D. (44024×![]() ,44024)
,44024)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com