
【题目】如图1,O为线段AB上一点,AB=6,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)若AO=4,
①当t=1秒时,OP= , S△ABP=;
②当△ABP是直角三角形时,求t的值;
(2)如图2,若点O为AB中点,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求AQBP的值.
【答案】
(1)2,3 ![]() ,解:②当△ABP是直角三角形时,a、若∠A=90°.∵∠BOC=60°且∠BOC>∠A,∴∠A≠90°,故此种情形不存在;b、若∠B=90°,如答图2所示:
,解:②当△ABP是直角三角形时,a、若∠A=90°.∵∠BOC=60°且∠BOC>∠A,∴∠A≠90°,故此种情形不存在;b、若∠B=90°,如答图2所示: ∵∠BOC=60°,∴∠BPO=30°,∴OP=2OB=4,又OP=2t,∴t=2;c、若∠APB=90°,如答图3所示:
∵∠BOC=60°,∴∠BPO=30°,∴OP=2OB=4,又OP=2t,∴t=2;c、若∠APB=90°,如答图3所示: 过点P作PD⊥AB于点D,则OD=OP?sin30°=t,PD=OP?sin60°=
过点P作PD⊥AB于点D,则OD=OP?sin30°=t,PD=OP?sin60°= ![]() t,∴AD=OA+OD=4+t,BD=OB﹣OD=2﹣t.在Rt△ABP中,由勾股定理得:PA2+PB2=AB2∴(AD2+PD2)+(BD2+PD2)=AB2,即[(4+t)2+(
t,∴AD=OA+OD=4+t,BD=OB﹣OD=2﹣t.在Rt△ABP中,由勾股定理得:PA2+PB2=AB2∴(AD2+PD2)+(BD2+PD2)=AB2,即[(4+t)2+( ![]() t)2]+[(2﹣t)2+(
t)2]+[(2﹣t)2+( ![]() t)2]=62,解方程得:t=
t)2]=62,解方程得:t= ![]() 或t=
或t= ![]() (负值舍去),∴t=
(负值舍去),∴t= ![]() .综上所述,当△ABP是直角三角形时,t=2或t=
.综上所述,当△ABP是直角三角形时,t=2或t= ![]() .
.
(2)解:如图中,作OE∥AP,交BP于点E.

∵AP=AB,
∴∠APB=∠B,
∴∠OEB=∠APB=∠B,
∵AQ∥BP,
∴∠QAB+∠B=180°.
又∵∠OEP+∠OEB=180°,
∴∠OEP=∠QAB,
又∵∠AOC=∠2+∠B=∠1+∠QOP,
∵∠B=∠QOP,
∴∠AOQ=∠OPE,
∴△QAO∽△OEP,
∴ ![]() =
= ![]() ,即AQEP=EOAO,
,即AQEP=EOAO,
由三角形中位线定理得OE=3,
∴AQEP=9,
∴AQBP=AQ2EP=2AQEP=18.
【解析】解:(1)①当t=1秒时,OP=2t=2×1=2.
如答图1,过点P作PD⊥AB于点D.

在Rt△POD中,PD=OPsin60°=2× ![]() =
= ![]() ,
,
∴S△ABP= ![]() ABPD=
ABPD= ![]() ×(4+2)×
×(4+2)× ![]() =3
=3 ![]() .
.
所以答案是2,3 ![]() .
.
【考点精析】关于本题考查的等腰三角形的性质和勾股定理的概念,需要了解等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】某车间为了改变管理松懈的状况,准备采取每天任务定额和超产有奖的措施,从而提高工作效率.下面是该车间15名工人过去一天中各自装配机器的数量(单位:台):
15,6,16,7,15,8,7,13,8,11,8,10,9,10,9.
请回答下列问题:
(1)这组数据的平均数、众数和中位数各是多少(结果精确到0.01台)?
(2)管理者应确定每人标准日产量为多少台比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果把一个奇数位的自然数各数为上的数字从最高位到个位依次排列,与从个位到最高位依次排列出的一串数字完全相同,相邻两个数位上的数字之差的绝对值相等(不等于0),且该数正中间的数字与其余数字均不同,我们把这样的自然数称为“阶梯数”,例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,且|1﹣2|=|2﹣3|=|3﹣2|=|2﹣1|=1,因此12321是一个“阶梯数”,又如262,85258,…,都是“阶梯数”,若一个“阶梯数”t从左数到右,奇数位上的数字之和为M,偶数位上的数字之和为N,记P(t)=2N﹣M,Q(t)=M+N.
(1)已知一个三位“阶梯数”t,其中P(t)=12,且Q(t)为一个完全平方数,求这个三位数;
(2)已知一个五位“阶梯数”t能被4整除,且Q(t)除以4余2,求该五位“阶梯数”t的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列方格纸中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)画出平移后的三角形;
.(1)画出平移后的三角形;
(2)若AB=5,则![]() = .
= .
(3)连接AA1,BB1, 根据“图形平移”的性质,得:线段AA1与线段BB1的数量关系和位置关系是: .
(4)求图中∠![]() AC+∠
AC+∠![]() BC的度数.
BC的度数.
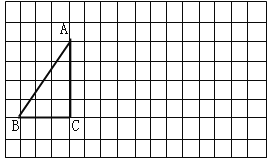
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
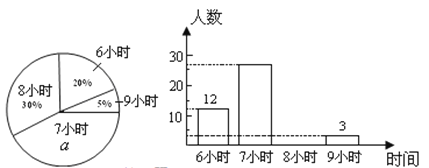
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;
(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程组
的方程组![]() ,以下结论:
,以下结论:
①![]() 时,方程组的解也是方程
时,方程组的解也是方程![]() 的解;
的解;
②论![]() 取什么实数,
取什么实数,![]() 的值始终不变;
的值始终不变;
③若![]() ,则
,则![]() 的最小值为
的最小值为![]() ;
;
请判断以上结论是否正确,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com