
����Ŀ�������һ������λ����Ȼ������Ϊ�ϵ����ִ����λ����λ�������У���Ӹ�λ�����λ�������г���һ��������ȫ��ͬ������������λ�ϵ�����֮��ľ���ֵ��ȣ�������0�����Ҹ������м���������������־���ͬ�����ǰ���������Ȼ����Ϊ������������������Ȼ��12321�������λ����λ�����ų���һ�������ǣ�1��2��3��2��1���Ӹ�λ�����λ�����ų���һ���������ǣ�1��2��3��2��1����|1��2|=|2��3|=|3��2|=|2��1|=1�����12321��һ������������������262��85258���������ǡ�������������һ������������t���������ң�����λ�ϵ�����֮��ΪM��ż��λ�ϵ�����֮��ΪN����P��t��=2N��M��Q��t��=M+N��
��1����֪һ����λ����������t������P��t��=12����Q��t��Ϊһ����ȫƽ�������������λ����
��2����֪һ����λ����������t�ܱ�4��������Q��t������4��2�������λ����������t�����ֵ����Сֵ��
���𰸡�
��1���⣺�衰��������t�İ�λΪx�����������IJ�Ϊk����t= ![]() ��
��
��M=a+a=2a��N=a+k��
��P��t��=2N��M=2��a+k����2a=2k=12��
��k=6��
��Q��t��=M+N=2a+a+k=3a+6Ϊһ����ȫƽ����������1��a��9��
��9��3a+6��33��
��3a+6=9��16��25��
��a=1��
��t=171��
��2���⣺��ij��λ������Ϊ ![]() ��
��
�� ![]() =
= ![]() =2778a+302k+
=2778a+302k+ ![]() ��
��
��2k��a��4�ı�����
��M=3a+2k��N=2A+2K��
��Q��t��=M+N=5a+4k��
�� ![]() =k+a+
=k+a+ ![]() ��
��
��a��2��4�ı�����
��1��a��9��
�ੁ1��a��2��7��
��a��2=0��4��
��a=2��6
��a=2ʱ�� ![]() Ϊ������0��2+2k��9��
������0��2+2k��9��
�ੁ1��k�� ![]() ��
��
��k=��1��3��
����t=21012��23432��25852��
��a=6ʱ�� ![]() Ϊ������0��6+2k��9��
������0��6+2k��9��
�ੁ3��k�� ![]() ��
��
��k=��1����3��
����t=63036��65456��67876��
���Ը���λ����������t�����ֵ��67876����Сֵ��21012��
����������1���衰��������t�İ�λΪx�����������IJ�Ϊk����t= a ( a + k ) a ���ɵ�M=a+a=2a��N=a+k������P��t��=12���õ�����k�ķ��̣������k=6���ٸ���Q��t��=3a+6Ϊһ����ȫƽ����������1��a��9������3a+6=9��16��25������a=1,�Ӷ��õ������λ����
��2����ij��λ������Ϊ a ( a + k ) ( a + 2 k ) ( a + k ) a ������ ![]() =
= ![]() =2778a+302k+
=2778a+302k+ ![]() ���ɵ�2k��a��4�ı���������M=3a+2k��N=2A+2K���ɵ�Q��t��=M+N=5a+4k����
���ɵ�2k��a��4�ı���������M=3a+2k��N=2A+2K���ɵ�Q��t��=M+N=5a+4k����![]() =k+a+
=k+a+![]() ,�ɵ�a��2��4�ı�����������ȫƽ�����Ķ���õ�a=2��6���ٷ�����������T��ֵ����һ���õ�����λ����������t�����ֵ����Сֵ��
,�ɵ�a��2��4�ı�����������ȫƽ�����Ķ���õ�a=2��6���ٷ�����������T��ֵ����һ���õ�����λ����������t�����ֵ����Сֵ��


 �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һСʱ�����������С���������������գ�ij����ί��֯��Ա���ڶ��ڳ������̵�̬�Ƚ���������������飬��Ҫ������̬�ȣ�A���˿ͳ�����ֹ��B��Ȱ˵�������ң�C�������ϰ������ֹ��D������ν������������������������������ͳ��ͼ���������ͼ�е���Ϣ�ش��������⣺
̬�� | A���˿ͳ�����ֹ | B��Ȱ˵�������� | C�������ϰ������ֹ | D������ν |
Ƶ���������� | 90 | 30 | 10 |
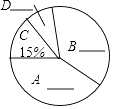
�������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1����γ����Ĺ������ˣ�
��2���뽫ͳ�Ʊ�������ͳ��ͼ����������
��3����ͳ��ͼ�С�B����������Ӧ��Բ�Ľ����ȣ�
��4����������120���ˣ����Ƹ���̬��Ϊ��A���˿ͳ�����ֹ���������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��4��x�ύ��A����2��0����B��8��0�����㣬��y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��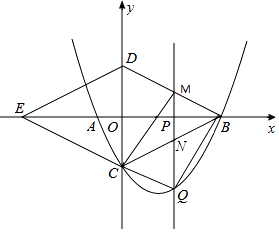
��1���������ߵĽ���ʽ��
��2������P���߶�OB���˶�ʱ��ֱ��l�ֱ�BD��BC�ڵ�M��N����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ���ʱ�����ж��ı���CQBM����״����˵�����ɣ�
��3������P���߶�EB���˶�ʱ���Ƿ���ڵ�Q��ʹ��BDQΪֱ�������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��
��![]() ��
��
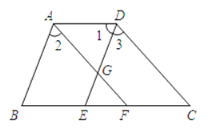
��1����˵��![]() ��
��
��2��AF��DC��λ�ù�ϵ��Σ� Ϊʲô��
�����DZ���Ľ����̣��벹��������
�⣺��1��![]() ������֪��
������֪��
![]() DEC
DEC![]() ��_____________________��
��_____________________��
��![]() ������֪��
������֪��
![]() _______����_____________________��
_______����_____________________��
![]() AB
AB![]() DE
DE![]() ��_____________________��
��_____________________��
��2��![]() ��DC��λ�ù�ϵ�ǣ�_______________
��DC��λ�ù�ϵ�ǣ�_______________![]() �������£�
�������£�
![]() ������֪��
������֪��
![]() AGD
AGD![]() ��_____________________��
��_____________________��
��![]() ������֪��
������֪��
![]() AGD
AGD![]()
![]() ��������
��������![]()
![]() _____
_____![]() ____
____![]() ��_____________________��
��_____________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=x2+bx+c��y=x��ͼ����ͼ��ʾ�������н�������ȷ���ǣ� ��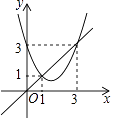
A.��1��x��3ʱ��x2+��b��1��x+c��0
B.b+c=1
C.3b+c=6
D.b2��4c��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����֪��A��2a2+3ab��2a��1��B����a2+ab��1��
��1����2A��3B��
��2����A+2B��ֵ��a��ȡֵ�أ���b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
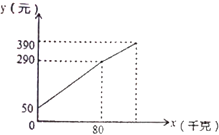
����Ŀ��һˮ�������������г���ÿǧ��1.8Ԫ����������ǧ�˵����Ͻ��dz��ۣ�Ϊ�˷��㣬������һЩ��Ǯ���ã����Ȱ��г����۳�һЩ���ֽ��۳��ۣ��۳�����ǧ����![]() �������г��е�Ǯ��
�������г��е�Ǯ��![]() Ԫ����������Ǯ���Ĺ�ϵ��ͼ��ʾ�����ͼ��ش��������⣺
Ԫ����������Ǯ���Ĺ�ϵ��ͼ��ʾ�����ͼ��ش��������⣺
��1��ũ���Դ���Ǯ�Ƕ��٣�
��2������ǰ��ÿǧ�����ϳ��۵ļ۸��Ƕ��٣�
��3���������ÿǧ���½�0.5Ԫ��ʣ����������꣬��ʱ�����е�Ǯ�������õ�Ǯ����390Ԫ������һ�������˶���ǧ�˵����ϣ�
��4���������ˮ������һ���˶���Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��OΪ�߶�AB��һ�㣬AB=6��OCΪ���ߣ��ҡ�BOC=60�㣬����P��ÿ��2����λ���ȵ��ٶȴӵ�O������������OC�������˶������˶�ʱ��Ϊt�룮
��1����AO=4��
�ٵ�t=1��ʱ��OP= �� S��ABP=��
�ڵ���ABP��ֱ��������ʱ����t��ֵ��
��2����ͼ2������OΪAB�е㣬��AP=ABʱ������A��AQ��BP����ʹ�á�QOP=��B����AQBP��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�ηֱ��ǹ��֡����ϡ����ࡢ��ɽ����̨��̨�գ�����Ϊ���ĶԳ�ͼ�ε��ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com