
����Ŀ����ͼ��������y=ax2+bx��4��x�ύ��A����2��0����B��8��0�����㣬��y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��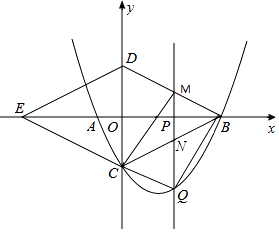
��1���������ߵĽ���ʽ��
��2������P���߶�OB���˶�ʱ��ֱ��l�ֱ�BD��BC�ڵ�M��N����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ���ʱ�����ж��ı���CQBM����״����˵�����ɣ�
��3������P���߶�EB���˶�ʱ���Ƿ���ڵ�Q��ʹ��BDQΪֱ�������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��x=0����ã�y=��4��
��C��0����4����
�������ߵĽ���ʽΪy=a��x+2����x��8��������C���������ã���16a=��4����ã�a= ![]() ��
��
�������ߵĽ���ʽΪy= ![]() ��x+2����x��8����y=
��x+2����x��8����y= ![]() x2��
x2�� ![]() x��4��
x��4��
��2���⣺�����εĶԳ��Կ�֪����D������Ϊ��0��4����
��ֱ��BD�Ľ���ʽΪy=kx+4������B���������ã�8k+4=0����ã�k=�� ![]() ��
��
��ֱ��BD�Ľ���ʽΪy=�� ![]() x+4��
x+4��
��l��x�ᣬ
���M��Q������ֱ��ǣ�m���� ![]() m+4������m��
m+4������m�� ![]() m2��
m2�� ![]() m��4����
m��4����
��MQ=DCʱ���ı���CQMDΪƽ���ı��Σ�
�ࣨ�� ![]() m+4������
m+4������ ![]() m2��
m2�� ![]() m��4��=8������ã�m2��4m=0�����m=4��m=0����ȥ����
m��4��=8������ã�m2��4m=0�����m=4��m=0����ȥ����
��ʱ���ı���CQBM��ƽ���ı��Σ�
���ı���CQBMΪƽ���ı��Σ�
��MD��CQ��MD=CQ��
��m=4ʱ��M������Ϊ��4��2����
��MΪBD���е㣬
��MD=MB��
��CQ=MB��
�֡�MB��CQ��
���ı���CQBMΪƽ���ı��Σ�
��3���⣺��QB�Ľ���ʽΪy=k1x+b1������B�͵�Q���������ã� 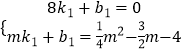 ��
��
��ã�k1= ![]() =
= ![]() ��m+2����
��m+2����
��QD�Ľ���ʽΪy=k2x+4������Q����������mk2+4= ![]() m2��
m2�� ![]() m��4��
m��4��
��ã�k2= ![]() ��
��
����QBD=90��ʱ���� ![]() ��
�� ![]() ��m+2��=��1����ã�m=6��
��m+2��=��1����ã�m=6��
��Q��6����4����
����QDB=90��ʱ���� ![]() ��
�� ![]() =��1�������ã�m2��14m��32=0�����m=��2��m=16����ȥ����
=��1�������ã�m2��14m��32=0�����m=��2��m=16����ȥ����
��Q����2��0����
��MΪԲ����MBΪ�뾶����M����M��������û�й����㣬
���DQB��90�㣮
������������Q��������6����4����2��0����
����������1�����ô���ϵ��������A��B��������������ʽ�����a��b���ɣ���2��Ҫʹ�ı���CQMD��ƽ���ı��Σ���MQ=DC=8�������� ![]() m+4������
m+4������ ![]() m2��
m2�� ![]() m��4��=8���������̣������m;��3������BDQΪֱ�������Σ���������ۣ���QBD=90����QDB=90�㣬������ֱ�ߵ�б�ʻ�Ϊ-1��������m�ķ��̣����m,����MΪԲ����MBΪ�뾶����M����M��������û�й����㣬��ˡ�DQB��90��.
m��4��=8���������̣������m;��3������BDQΪֱ�������Σ���������ۣ���QBD=90����QDB=90�㣬������ֱ�ߵ�б�ʻ�Ϊ-1��������m�ķ��̣����m,����MΪԲ����MBΪ�뾶����M����M��������û�й����㣬��ˡ�DQB��90��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧѧ�����е��������У����꼶![]() ��ѧ�����ǰ�ӣ������ٶ�Ϊ4ǧ��
��ѧ�����ǰ�ӣ������ٶ�Ϊ4ǧ��![]() Сʱ����
Сʱ����![]() ���ѧ����ɺ�ӣ��ٶ�Ϊ6ǧ��
���ѧ����ɺ�ӣ��ٶ�Ϊ6ǧ��![]() Сʱ��ǰ�ӳ���1Сʱ��Ӳų�����ͬʱ�����һ������Ա�����г�������֮�䲻��ϵ��������磬���ﳵ���ٶ�Ϊ10ǧ��
Сʱ��ǰ�ӳ���1Сʱ��Ӳų�����ͬʱ�����һ������Ա�����г�������֮�䲻��ϵ��������磬���ﳵ���ٶ�Ϊ10ǧ��![]() Сʱ��
Сʱ��
![]() �����ǰ����Ҫ�ʱ�䣿
�����ǰ����Ҫ�ʱ�䣿
![]() �����ǰ�ӵ�ʱ���ڣ�����Ա�ߵ�·���Ƕ��٣�
�����ǰ�ӵ�ʱ���ڣ�����Ա�ߵ�·���Ƕ��٣�
![]() ���꼶
���꼶![]() ���������Сʱ���������2ǧ�ף�
���������Сʱ���������2ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������a��b��c�������ϵ�λ����ͼ��ʾ���ұ�ʾ��a�ĵ㡢��b�ĵ���ԭ��ľ�����ȣ�
![]()
��1������<������0��a, b, ��1
��2��|b��1|��|a��1|��___
��3������|a ��b|��|a��c|��|b|��|b��c|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˸ı������и��״��������ȡÿ������ͳ����н��Ĵ�ʩ���Ӷ���߹���Ч�ʣ������Ǹó���15�����˹�ȥһ���и���װ�����������(��λ��̨)��
15��6��16��7��15��8��7��13��8��11��8��10��9��10��9.
��ش��������⣺
(1)�������ݵ�ƽ��������������λ�����Ƕ���(�����ȷ��0.01̨)?
(2)������Ӧȷ��ÿ�˱��ղ���Ϊ����̨�ȽϺ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˷�װ������һ�ּп˺�T�����п�ÿ������![]() Ԫ��T��ÿ������
Ԫ��T��ÿ������![]() Ԫ.�����ڿ�չ������ڼ䣬��ͻ��ṩ�����Żݷ���������һ���п���һ��T�������п˺�T���������۵�
Ԫ.�����ڿ�չ������ڼ䣬��ͻ��ṩ�����Żݷ���������һ���п���һ��T�������п˺�T���������۵�![]() ����.��ij�ͻ�Ҫ���÷�װ������п�
����.��ij�ͻ�Ҫ���÷�װ������п�![]() ����T��
����T��![]() ����
����![]() ��.
��.
��1�����ÿͻ������������п��踶��________Ԫ��T���踶��________Ԫ���ú�![]() ��ʽ�ӱ�ʾ�������ÿͻ������������п��踶��______Ԫ��T���踶��______Ԫ���ú�
��ʽ�ӱ�ʾ�������ÿͻ������������п��踶��______Ԫ��T���踶��______Ԫ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2����![]() ��ͨ������˵���������������������ַ��������Ϊ���㣿
��ͨ������˵���������������������ַ��������Ϊ���㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��MN��AB���ѡ�ABC���������֣���C��ֱ��AB�ϣ���O��ֱ��MN�ϣ����O�ǡ�ABC�ģ� ��
A.����
B.����
C.����
D.����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D�ǡ�ABC��һ�㣬BD��CD��AD=6��BD=4��CD=3��E��F��G��H�ֱ���AB��AC��CD��BD���е㣬���ı���EFGH���ܳ��ǣ� ��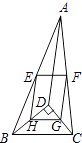
A.7
B.9
C.10
D.11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������һ������λ����Ȼ������Ϊ�ϵ����ִ����λ����λ�������У���Ӹ�λ�����λ�������г���һ��������ȫ��ͬ������������λ�ϵ�����֮��ľ���ֵ��ȣ�������0�����Ҹ������м���������������־���ͬ�����ǰ���������Ȼ����Ϊ������������������Ȼ��12321�������λ����λ�����ų���һ�������ǣ�1��2��3��2��1���Ӹ�λ�����λ�����ų���һ���������ǣ�1��2��3��2��1����|1��2|=|2��3|=|3��2|=|2��1|=1�����12321��һ������������������262��85258���������ǡ�������������һ������������t���������ң�����λ�ϵ�����֮��ΪM��ż��λ�ϵ�����֮��ΪN����P��t��=2N��M��Q��t��=M+N��
��1����֪һ����λ����������t������P��t��=12����Q��t��Ϊһ����ȫƽ�������������λ����
��2����֪һ����λ����������t�ܱ�4��������Q��t������4��2�������λ����������t�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽���и��꼶ѧ��ÿ���ƽ��˯��ʱ�䣨��λ��h����ȷ��1 h�������������˲���ѧ�������õõ������ݻ���������������������ͳ��ͼ��
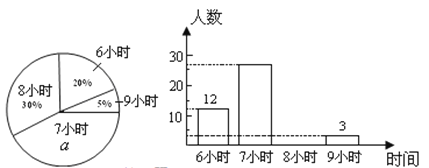
�������ͼ���ṩ����Ϣ���ش��������⣺
��1���������ͳ��ͼ�аٷ���![]() ��ֵΪ_______��������ѧ������Ϊ______��
��ֵΪ_______��������ѧ������Ϊ______��
��2�����ƽ��˯��ʱ��Ϊ8Сʱ������������ȫ����ͼ��
��3������ⲿ��ѧ����ƽ��˯��ʱ���ƽ������
��4�������У����ѧ��1200�����������˯�߲��㣨����8Сʱ����ѧ����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com