
【题目】函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )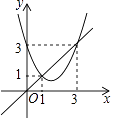
A.当1<x<3时,x2+(b﹣1)x+c<0
B.b+c=1
C.3b+c=6
D.b2﹣4c>0
【答案】A
【解析】解:∵抛物线与直线y=x相交于点(1,1),(3,3),
∴当1<x<3时,x2+bx+c<x,
即x2+(b﹣1)x+c<0,所以A选项符合题意;
把(1,1)代入y=x2+bx+c得1+b+c=1,
∴b+c=0,所以B选项错误;
把(3,3)代入y=x2+bx+c得9+3b+c=3,
∴3b+c=6,所以C选项不符合题意;
∵抛物线与x轴没有交点,
∴△=b2﹣4ac<0,所以D不符合题意.
所以答案是:A.
【考点精析】根据题目的已知条件,利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】完成下面的证明.
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新兴服装厂生产一种夹克和T恤,夹克每件定价![]() 元,T恤每件定价
元,T恤每件定价![]() 元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的
元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的![]() 付款.现某客户要到该服装厂购买夹克
付款.现某客户要到该服装厂购买夹克![]() 件,T恤
件,T恤![]() 件(
件(![]() ).
).
(1)若该客户按方案①购买,夹克需付款________元,T恤需付款________元(用含![]() 的式子表示);若该客户按方案②购买,夹克需付款______元,T恤需付款______元(用含
的式子表示);若该客户按方案②购买,夹克需付款______元,T恤需付款______元(用含![]() 的式子表示);
的式子表示);
(2)若![]() ,通过计算说明按方案①、方案②哪种方案购买较为合算?
,通过计算说明按方案①、方案②哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是( )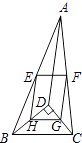
A.7
B.9
C.10
D.11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明一家到某拓展基地训练,![]() 小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发
小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发![]() 他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地
他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地![]() 如图是他们离家的距离s
如图是他们离家的距离s![]() km
km![]() 与小明离家的时问t
与小明离家的时问t![]() 的关系图.
的关系图.
(1)请根据图象,回答问题:
①图中点A表示的意义是 .
②当爸爸第一次到达度假村后,小明离度假村的距离是______ km;
(2)爸爸在返回家的途中与小明相遇时,小明离家的距离是多少?
(3)整个运动过程中(双方全部到达会合时,视为运动结束),请直接写出小明与爸爸相距24km时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果把一个奇数位的自然数各数为上的数字从最高位到个位依次排列,与从个位到最高位依次排列出的一串数字完全相同,相邻两个数位上的数字之差的绝对值相等(不等于0),且该数正中间的数字与其余数字均不同,我们把这样的自然数称为“阶梯数”,例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,且|1﹣2|=|2﹣3|=|3﹣2|=|2﹣1|=1,因此12321是一个“阶梯数”,又如262,85258,…,都是“阶梯数”,若一个“阶梯数”t从左数到右,奇数位上的数字之和为M,偶数位上的数字之和为N,记P(t)=2N﹣M,Q(t)=M+N.
(1)已知一个三位“阶梯数”t,其中P(t)=12,且Q(t)为一个完全平方数,求这个三位数;
(2)已知一个五位“阶梯数”t能被4整除,且Q(t)除以4余2,求该五位“阶梯数”t的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
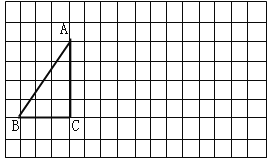
【题目】将下列方格纸中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)画出平移后的三角形;
.(1)画出平移后的三角形;
(2)若AB=5,则![]() = .
= .
(3)连接AA1,BB1, 根据“图形平移”的性质,得:线段AA1与线段BB1的数量关系和位置关系是: .
(4)求图中∠![]() AC+∠
AC+∠![]() BC的度数.
BC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将![]() 化为分数形式
化为分数形式
由于![]() =0.777…,设x=0.777…①
=0.777…,设x=0.777…①
则10x=7.777…②
②﹣①得9x=7,解得x=![]() ,于是得
,于是得![]() =
=![]() .
.
同理可得![]() =
=![]() ,
,![]() =1+
=1+![]() =1+
=1+![]() ,
,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(基础训练)
(1)![]() = ,
= ,![]() = ;
= ;
(2)将![]() 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;
(能力提升)
(3)![]() = ,
= ,![]() = ;
= ;
(注:![]() =0.315315…,
=0.315315…,![]() =2.01818…)
=2.01818…)
(探索发现)
(4)①试比较![]() 与1的大小:
与1的大小:![]() 1(填“>”、“<”或“=”)
1(填“>”、“<”或“=”)
②若已知![]() =
=![]() ,则
,则![]() = .
= .
(注:![]() =0.285714285714…)
=0.285714285714…)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com