
【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.

【答案】(1)72°(2)54°或126°
【解析】
(1)依据垂线的定义,即可得到∠DOE的度数,再根据角平分线的定义,即可得到∠BOD的度数,进而得出结论;
(2)分两种情况讨论,依据垂线的定义以及角平分线的定义,即可得到∠AOG的度数.
(1)∵OF⊥CD,∠EOF=54°,
∴∠DOE=90°﹣54°=36°,
又∵OE平分∠BOD,
∴∠BOD=2∠DOE=72°,
∴∠AOC=72°;
(2)如图,若OG在∠AOD内部,则
由(1)可得,∠BOE=∠DOE=36°,
又∵∠GOE=90°,
∴∠AOG=180°﹣90°﹣36°=54°;
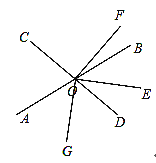
如图,若OG在∠COF内部,则
由(1)可得,∠BOE=∠DOE=36°,
∴∠AOE=180°﹣36°=144°,
又∵∠GOE=90°,
∴∠AOG=360°﹣90°﹣144°=126°.
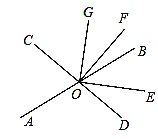
综上所述,∠AOG的度数为54°或126°.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为![]() 千米
千米![]() 小时,同时一辆出租车从乙城开往甲城,车速为90千米
小时,同时一辆出租车从乙城开往甲城,车速为90千米![]() 小时,设客车行驶时间为
小时,设客车行驶时间为![]() 小时
小时![]()
![]() 当
当![]() 时,客车与乙城的距离为多少千米
时,客车与乙城的距离为多少千米![]() 用含a的代数式表示
用含a的代数式表示![]()
![]() 已知
已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米
,丙城在甲、乙两城之间,且与甲城相距260千米
![]() 求客车与出租车相距100千米时客车的行驶时间;
求客车与出租车相距100千米时客车的行驶时间;![]() 列方程解答
列方程解答![]()
![]() 已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
已知客车和出租车在甲、乙之间的服务站M处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在M处换乘客车返回乙城.
试通过计算,分析小王选择哪种方案能更快到达乙城?
查看答案和解析>>
科目:初中数学 来源: 题型:
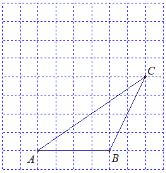
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC向左平移2个单位,再向上平移3个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: ;
(3)画出△ABC中BC边上的中线AD;
(4)△ACD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于 ![]() 的一元二次方程 x2+(2m-1)x+m2=0有两个实数根 x1 和 x2 .
的一元二次方程 x2+(2m-1)x+m2=0有两个实数根 x1 和 x2 .
(1)求实数 m 的取值范围;
(2)当 x12-x22 时,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,DE垂直平分AB,分别交AB、BC于点D、E,AP平分∠BAC,与DE的延长线交于点P.

(1)求PD的长度;
(2)连结PC,求PC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1对应的函数表达式为y=2x-2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1,l2交于点C(m,2).
(1)求点D,点C的坐标;
(2)求直线l2对应的函数表达式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x,y的二元一次方程组![]() 的解.
的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠COE=90°,OF平分∠AOE.
(1)若∠COF=40°,求∠BOE的度数.
(2)若∠COF=α(0°<α<90°),则∠BOE=______(用含α的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com