
【题目】如图,直线l1对应的函数表达式为y=2x-2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1,l2交于点C(m,2).
(1)求点D,点C的坐标;
(2)求直线l2对应的函数表达式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x,y的二元一次方程组![]() 的解.
的解.

【答案】(1) 点D (1,0),点C (2,2);(2) y=-x+4 ;(3)3;(4)![]() .
.
【解析】
(1)把 y=0代入直线l1的解析式即可求出点D的坐标,把C(m,2)代入C(m,2)可求出m的值,从而得出点C的坐标;
(2)根据点C,B在直线l2上,利用待定系数法即可求出;
(3)求出点A坐标,根据三角形面积公式可求出△ADC的面积;
(4) 二元一次方程组 ![]() 的解即两个二次函数的交点坐标.
的解即两个二次函数的交点坐标.
解:(1)∵点D是直线l1:y=2x-2与x轴的交点,
∴令y=0,则0=2x-2,
∴x=1,
∴点D的坐标为(1,0),
∵点C在直线l1:y=2x-2上,
∴2=2m-2,
∴m=2,
∴点C的坐标为(2,2).
(2)∵点C(2,2),B(3,1)在直线l2上,
∴![]() 解得
解得![]()
∴直线l2对应的函数表达式为y=-x+4.
(3)∵点A是直线l2与x轴的交点,
∴令y=0,则0=-x+4,
解得x=4,即点A(4,0),
∴AD=4-1=3,
∴S△ADC=![]() ×3×2=3.
×3×2=3.
(4)由题图可知![]() 的解为
的解为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ).

A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
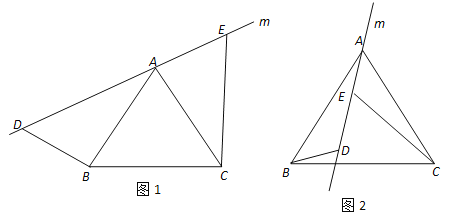
【题目】探索与证明:(1)如图1,直线m经过正三角形ABC的顶点A,在直线m上取两点 D,E,使得∠ADB=60°,∠AEC=60°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明;
(2)将(1)中的直线m绕点A逆时针方向旋转一个角度到如图2的位置,并使∠ADB=120°,∠AEC=120°.通过观察或测量,请直接写出线段BD,CE与DE之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是网格图,每个小正方形的边长均为1.△ABC(“△”表示“三角形”)是格点三角形(即每个顶点都在小正方形的顶点上),它在坐标平面内平移,得到△PEF,点A平移后落在点P的位置上.
(1)请你在图中画出△PEF,并写出顶点P、E、F的坐标;
(2)说出△PEF是由△ABC分别经过怎样的平移得到的?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF. 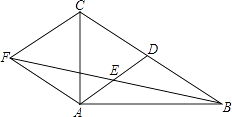
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售![]() ,
,![]() 两种型号的新能源汽车。上周售出1辆
两种型号的新能源汽车。上周售出1辆![]() 型车和3辆
型车和3辆![]() 型车,销售额为96万元,本周已售出2辆
型车,销售额为96万元,本周已售出2辆![]() 型车和1辆
型车和1辆![]() 型车,销售额为62万元。
型车,销售额为62万元。
(1)求每辆![]() 型车和
型车和![]() 型车的售价各为多少?
型车的售价各为多少?
(2)随着汽车限购政策的推行,预计下周起![]() ,
,![]() 两种型号的汽车价格在原有的基础均有上涨,若
两种型号的汽车价格在原有的基础均有上涨,若![]() 型汽车价格上涨m%,
型汽车价格上涨m%,![]() 型汽车价格上涨3m%,则同时购买一台
型汽车价格上涨3m%,则同时购买一台![]() 型车和一台
型车和一台![]() 型车的费用比涨价前多12%,求
型车的费用比涨价前多12%,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com