
【题目】如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC. 
(1)求证:AC=BD;
(2)若sin∠C= ![]() ,BC=12,求AD的长.
,BC=12,求AD的长.
【答案】
(1)证明:∵AD是BC上的高,
∴AD⊥BC,
∴∠ADB=90°,∠ADC=90°,
在Rt△ABD和Rt△ADC中,
∵tanB= ![]() ,cos∠DAC=
,cos∠DAC= ![]() ,
,
又∵tanB=cos∠DAC,
∴ ![]() =
= ![]() ,
,
∴AC=BD.
(2)解:在Rt△ADC中, ![]() ,
,
故可设AD=12k,AC=13k,
∴CD= ![]() =5k,
=5k,
∵BC=BD+CD,又AC=BD,
∴BC=13k+5k=18k
由已知BC=12,
∴18k=12,
∴k= ![]() ,
,
∴AD=12k=12× ![]() =8.
=8.
【解析】(1)由于tanB=cos∠DAC,所以根据正切和余弦的概念证明AC=BD;(2)设AD=12k,AC=13k,然后利用题目已知条件即可解直角三角形.
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线l1对应的函数表达式为y=2x-2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1,l2交于点C(m,2).
(1)求点D,点C的坐标;
(2)求直线l2对应的函数表达式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x,y的二元一次方程组![]() 的解.
的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出了电脑上网包月月制,每月收取费用y(元)与上网时间x(小时)之间的函数关系式如图所示,其中OA是线段,AC是射线.
(1)当x≥30时,求y与x之间的函数关系式;
(2)若小李4月份上网时间为20小时,他应付多少元上网费用;
(3)若小李5月份上网费用为75元,则他在5月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
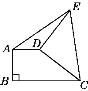
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BI,CI分别平分∠ABC,∠ACB,过I点作DE∥BC,交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△ACI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC.其中正确的是( )

A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在等边△ABC的边BC上. 
(1)把△ACD绕点A顺时针旋转,使点C与点B重合,画出旋转后的△ABD′;
(2)如果AC=4,CD=1,求(1)中点D旋转所走过的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,这是一个五角星ABCDE,你能计算出∠A+∠B+∠C+∠D+∠E的度数吗?为什么?(必须写推理过程)
(2)如图2,如果点B向右移动到AC上,那么还能求出∠A+∠DBE+∠C+∠D+∠E的大小吗?若能结果是多少?(可不写推理过程)
(3)如图,当点B向右移动到AC的另一侧时,上面的结论还成立吗?
(4)如图4,当点B、E移动到∠CAD的内部时,结论又如何?根据图3或图4,说明你计算的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com