
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.

【答案】(1)AF=BD;证明见解析;(2)成立,证明见解析;(3)Ⅰ.AF+BF′=AB;证明见解析;Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′;证明见解析.
【解析】解:(1)AF=BD。证明如下:
∵△ABC是等边三角形(已知),∴BC=AC,∠BCA=60°(等边三角形的性质)。
同理知,DC=CF,∠DCF=60°。
∴∠BCA﹣∠DCA=∠DCF﹣DCA,即∠BCD=∠ACF。
在△BCD和△ACF中,∵BC=AC,∠BCD=∠ACF,DC=CF,
∴△BCD≌△ACF(SAS)。∴BD=AF(全等三角形的对应边相等)。
(2)AF=BD仍然成立。
(3)Ⅰ.AF+BF′=AB。证明如下:
由(1)知,△BCD≌△ACF(SAS),则BD=AF。
同理△BCF′≌△ACD(SAS),则BF′=AD。
∴AF+BF′=BD+AD=AB。
Ⅱ.Ⅰ中的结论不成立,新的结论是AF=AB+BF′。证明如下:
在△BCF′和△ACD中,∵BC=AC,∠BC F′=∠ACD,F′C=DC,
∴△BCF′≌△ACD(SAS)。∴BF′=AD(全等三角形的对应边相等)。
又由(2)知,AF=BD,∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′。
(1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定理SAS可以证得△BCD≌△ACF;然后由全等三角形的对应边相等知AF=BD。
(2)通过证明△BCD≌△ACF,即可证明AF=BD。
(3)Ⅰ.AF+BF′=AB;利用全等三角形△BCD≌△ACF(SAS)的对应边BD=AF;同理△BCF′≌△ACD(SAS),则BF′=AD,所以AF+BF′=AB。
Ⅱ.Ⅰ中的结论不成立,新的结论是AF=AB+BF′:通过证明△BCF′≌△ACD(SAS),则BF′=AD(全等三角形的对应边相等),再结合(2)中的结论即可证得AF=AB+BF′


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(﹣6,7)、(﹣3,0)、(0,3).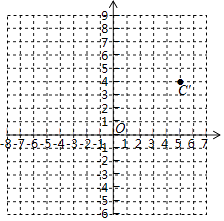
(1)画出△ABC,并求△ABC的面积;在△ABC中,点C经过平移后的对应点为C′(5,4),将△ABC作同样的平移得到△A′B′C′,画出平移后的△A′B′C′,并写出点A′,B′的坐标;
(2)P(﹣3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,﹣3),则m= , n= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至2020年4月23日,全球新型冠状病毒肺炎累计确诊人数超过2550000人,这个数据用科学计数法表示为( )
A.2.55×106B.25.5×105C.2.55×107D.0.255×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将抛物线y=x2﹣2x﹣1先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是( )
A.y=(x+1)2+1B.y=(x﹣3)2+1C.y=(x﹣3)2﹣5D.y=(x+1)2+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com