
【题目】如图,O为直线AB上一点,∠COE=90°,OF平分∠AOE.
(1)若∠COF=40°,求∠BOE的度数.
(2)若∠COF=α(0°<α<90°),则∠BOE=______(用含α的式子表示).

【答案】(1)∠BOE=80°;(2)∠BOE=2α.
【解析】
(1)和(2)思路是一样的,因为∠BOE=∠AOB-∠AOE,要想求∠BOE的度数,只要求出∠AOE即可,根据题中已知条件,即可解答.
(1)因为∠EOF=∠COE-∠COF=90°-40°=50°,
又因为OF平分∠AOE,
所以∠AOE=2∠EOF=100°
所以∠BOE=∠AOB-∠AOE=180°-100°=80°;
(2)∠EOF=∠COE-∠COF=90°-α,
因为OF平分∠AOE,
所以∠AOE=2∠EOF=2(90°-α)=180°-2α,
所以∠BOE=∠AOB-∠AOE=180°-(180°-2α)=2α.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )
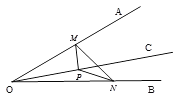
A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外圴相同.
(1)从箱子里任意摸出一个球是白球的概率是多少?
(2)从箱子里任意摸出一个球,不将它放回,搅均后再摸出一球,求两次摸出的球都是白球的概率,并画出树状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E是圆内的两条弦AB、CD的交点,直线EF∥CB,交AD的延长线于F,FG切圆于G.连接AG、DG.
求证:
(1)△DFE∽△EFA
(2)EF=FG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发沿图中某一个扇形顺时针匀速运动,设∠APB=y(单位:度),如果y与点P运动的时间x(单位:秒)的函数关系的图象大致如图2所示,那么点P的运动路线可能为( )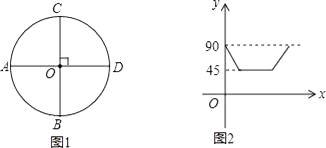
A.O→B→A→O
B.O→A→C→O
C.O→C→D→O
D.O→B→D→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A. OA=OC,OB=ODB. OA=OC,AB∥CD
C. AB=CD,OA=OCD. ∠ADB=∠CBD,∠BAD=∠BCD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com