
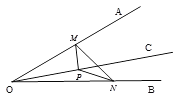
【题目】如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )
A. 2 B. 4 C. ![]() D.
D. ![]()
【答案】B
【解析】
作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,与OA的交点即为点M,与OB的交点即为点N,则此时M、N符合题意,求出线段P1P2的长即可.
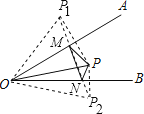
解:作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,
与OA的交点即为点M,与OB的交点即为点N,此时△PMN的最小周长
∵点P关于OA的对称点为P1,关于OB的对称点为P2,连结OP1、OP2,
∴PM= P1M,OP=O P1,∠P1OA=∠POA;
∵点P关于OB的对称点为P2,
∴PN= P2N,OP=O P2,∠P2OB=∠POB,
∴OP1=OP2=OP=4,
∠P1OP2=∠P1OA+∠POA+∠POB+∠P2OB=2∠POA+2∠POB=2∠AOB=60°,
∴△OP1P2是等边三角形,
∴P1P2=OP1=4,
∴△PMN的最小周长为PM+MN+PN=P1M+MN+P2N=P1P2=4
即△PMN的周长的最小值是4.
故选:B.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
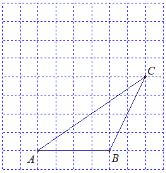
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC向左平移2个单位,再向上平移3个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: ;
(3)画出△ABC中BC边上的中线AD;
(4)△ACD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1对应的函数表达式为y=2x-2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1,l2交于点C(m,2).
(1)求点D,点C的坐标;
(2)求直线l2对应的函数表达式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x,y的二元一次方程组![]() 的解.
的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
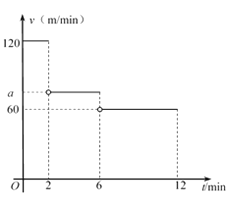
【题目】小明从家出发,沿一条直道散步到离家450 m的邮局,经过一段时间原路返回,刚好在第12 min回到家中.设小明出发第t min时的速度为v m/min,v与t之间的函数关系如图所示(图中的空心圈表示不包含这一点).
(1)小明出发第2 min时离家的距离为 m;
(2)当2< t ≤6时,求小明的速度a;
(3)求小明到达邮局的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品![]() 件(
件(![]() >0),购买两种商品共花费
>0),购买两种商品共花费![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式(写出自变量
的函数关系式(写出自变量![]() 的取值范围);
的取值范围);
(2)试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲组的![]() 名工人12月份完成的总工作量比此月人均定额的
名工人12月份完成的总工作量比此月人均定额的![]() 倍多
倍多![]() 件,乙组的
件,乙组的![]() 名工人12月份完成的总工作量比此月人均定额的
名工人12月份完成的总工作量比此月人均定额的![]() 倍少
倍少![]() 件.
件.
(1)如果两组工人实际完成的此月人均工作量相等,那么此月的人均定额是多少件?
(2)如果甲组工人实际完成的此月人均工作量比乙组工人实际完成的此月人均工作量少3件,那么此月人均定额是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠COE=90°,OF平分∠AOE.
(1)若∠COF=40°,求∠BOE的度数.
(2)若∠COF=α(0°<α<90°),则∠BOE=______(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司以每吨![]() 元的价格收购了
元的价格收购了![]() 吨某种药材,若直接在市场上销售,每吨的售价是
吨某种药材,若直接在市场上销售,每吨的售价是![]() 元.该公司决定加工后再出售,相关信息如下表所示:
元.该公司决定加工后再出售,相关信息如下表所示:
工艺 | 每天可加工药材的吨数 | 成品率 | 成品售价 (元/吨) |
粗加工 | 14 | 80% | 6000 |
精加工 | 6 | 60% | 11000 |
(注:①成品率80%指加工100吨原料能得到80吨可销售药材;②加工后的废品不产生效益.)
受市场影响,该公司必须在![]() 天内将这批药材加工完毕.
天内将这批药材加工完毕.
(1)若全部粗加工,可获利_______________________元;
(2)若尽可能多的精加工,剩余的直接在市场上销售,可获利_____________元;
(3)若部分粗加工,部分精加工,恰好![]() 天完成,求可获利多少元?
天完成,求可获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com