练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】同时掷两枚标有数字1～6的正方形骰子，数字和为1的概率是 。

    【答案】0
    【解析】列表得：

    1

    2

    3

    4

    5

    6

    1

    （1，1）

    （2，1）

    （3，1）

    （4，1）

    （5，1）

    （6，1）

    2

    （1，2）

    （2，2）

    （3，2）

    （4，2）

    （5，2）

    （6，2）

    3

    （1，3）

    （2，3）

    （3，3）

    （4，3）

    （5，3）

    （6，3）

    4

    （1，4）

    （2，4）

    （3，4）

    （4，4）

    （5，4）

    （6，4）

    5

    （1，5）

    （2，5）

    （3，5）

    （4，5）

    （5，5）

    （6，5）

    6

    （1，6）

    （2，6）

    （3，6）

    （4，6）

    （5，6）

    （6，6）

    ∵共有36种等可能的结果，数字和为1的有0种情况，

    ∴故数字和为1概率是： ．


    【考点精析】根据题目的已知条件，利用可能性的大小和概率公式的相关知识可以得到问题的答案，需要掌握一般地，随机事件发生的可能性是有大小的，不同的随机事件发生的可能性的大小有可能不同；一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=m/n．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】数轴上点A对应的数为a，点B对应的数为b，且多项式﹣x2y﹣xy2﹣2xy+5的次数为a，常数项为b．

    （1）直接写出a、b的值；

    （2）数轴上点A、B之间有一动点P（不与A、B重合），若点P对应的数为x，试化简：|2x+6|+4|x﹣5|﹣|6﹣x|+|3x﹣9|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（给出定义）

    数轴上顺次有三点A、C、B,若点C到点A的距离是点C到点B的距离的3倍,我们就称点C是(A、B)的“梦想点”例如:图①中,点A、B表示的数分别为-2、2,表示数1的点C是(A、B)的“梦想点”；图②中,点A、B表示对的数分别为-2、2，表示-1的点C是(B、A)的“梦想点.

    （解决问题）

    (1)若数轴上M、N两点所表示的数分别为且满足求出(M、N)的“梦想点”表示的数；

    (2)如图③,在数轴上点A、B表示的数分别为-15和65,点P从点A出发沿数轴向右运动:

    ①若点P运动到点B停止,则当P、A、B中恰好有一个点为其余两个点的“梦想点”时,求这个点表示的数；

    ②若点P运动到B后,继续沿数轴向右运动的过程中,是否还存在点P、A、B中恰好有一个点为其余两点的“梦想点”的情况?若存在,请直接写出此时以PA、PB为邻边长的长方形的周长；若不存在,请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线AB、CD相交于点O，OE平分∠BOD．OF⊥CD，垂足为O，若∠EOF＝54°．

    （1）求∠AOC的度数；

    （2）作射线OG⊥OE，试求出∠AOG的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数 的图象如图所示，有下列4个结论，其中正确的结论是（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若正整数 使得在计算 的过程中，各数位不产生进位现象，则称 为“本位数.现从所有大于0,且小于100的“本位数”中，随机抽取一个数，抽到偶数的概率为= .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°,AD是∠BAC的平分线，O是AB上一点,以OA为半径的⊙O经过点D。

    （1）求证：BC是⊙O切线；
    （2）若BD=5,DC=3,求AC的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠AOB=30°，OC为∠AOB内部一条射线，点P为射线OC上一点，OP=4，点M、N分别为OA、OB边上动点，则△MNP周长的最小值为( )

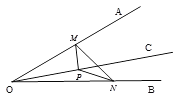
    A. 2 B. 4 C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，AD，BC是⊙O的两条互相垂直的直径，点P从点O出发沿图中某一个扇形顺时针匀速运动，设∠APB=y（单位：度），如果y与点P运动的时间x（单位：秒）的函数关系的图象大致如图2所示，那么点P的运动路线可能为（ ）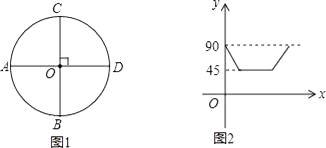

    A.O→B→A→O
    B.O→A→C→O
    C.O→C→D→O
    D.O→B→D→O

    查看答案和解析>>

    同步练习册答案