【题目】已知二次函数 
的图象如图所示，有下列4个结论，其中正确的结论是（ ）
A.
B.
C.
D.
【答案】C
【解析】抛物线的开口向下，则a＜0；…①
抛物线的对称轴为x=1，则- 
=1，b=-2a；…②
抛物线交y轴于正半轴，则c＞0；…③
抛物线与x轴有两个不同的交点，则：△=b2-4ac＞0；
由②知：b＞0，b+2a=0；
又由①③得：abc＜0；
由图知：当x=-1时，y＜0；即a-b+c＜0，b＞a+c；
故答案为：C．
根据抛物线的开口方向，对称轴的位置及抛物线与y轴的交点情况，可知a＜0、c＞0、b＞0，即可对A作出判断；根据对称轴x=1，可得出b+2a=0，可对B作出判断；将b > a + c变形为a-b+c＜0，根据x=-1，即可作出判断；根据抛物线与x轴的交点个数可对D作出判断。
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案科目：初中数学 来源： 题型：
【题目】如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1 ， O2 ， O3 ， … 组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒 
个单位长度，则第2016秒时，点P的坐标是
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在ABCD中，E，F分别是边AD，BC上的点，且AE=CF，直线EF分别交BA的延长线、DC的延长线于点G，H，交BD于点O．
（1）求证：△ABE≌△CDF；
（2）连接DG，若DG=BG，则四边形BEDF是什么特殊四边形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于 
的一元二次方程 x2+（2m-1）x+m2=0有两个实数根 x1 和 x2 ．
（1）求实数 m 的取值范围；
（2）当 x12-x22 时，求 m 的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠BAC=90°，AD⊥BC，垂足为点 D.下列说法中：①∠B的余角只有∠BAD；②∠B=∠C；③线段 AB 的长度表示点 B 到直线 AC 的距离；④AB·AC=BC·AD；一定正确的有( )
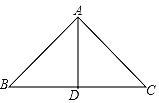
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目：初中数学 来源： 题型：
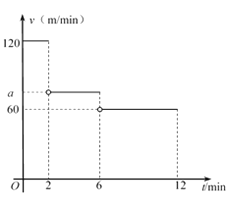
【题目】小明从家出发，沿一条直道散步到离家450 m的邮局，经过一段时间原路返回，刚好在第12 min回到家中．设小明出发第t min时的速度为v m/min，v与t之间的函数关系如图所示(图中的空心圈表示不包含这一点)．
(1)小明出发第2 min时离家的距离为 m；
(2)当2＜ t ≤6时，求小明的速度a；
(3)求小明到达邮局的时间．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)如图1，把△ABC沿DE折叠，使点A落在点A’处，试探索∠1+∠2与∠A的关系．（证明）．
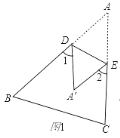
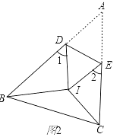
(2)如图2，BI平分∠ABC，CI平分∠ACB，把△ABC折叠，使点A与点I重合，若∠1+∠2=130°，求∠BIC的度数；
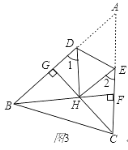
(3)如图3，在锐角△ABC中，BF⊥AC于点F，CG⊥AB于点G，BF、CG交于点H，把△ABC折叠使点A和点H重合，试探索∠BHC与∠1+∠2的关系，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
