Question

【题目】“戒烟一小时，健康亿人行”，今年国际无烟日，某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查，主要由四种态度：A．顾客出面制止；B．劝说进吸烟室；C．超市老板出面制止；D．无所谓．他将调查结果绘制了两幅不完整的统计图．请你根据图中的信息回答下列问题：

态度	A．顾客出面制止	B．劝说进吸烟室	C．超市老板出面制止	D．无所谓
频数（人数）	90		30	10

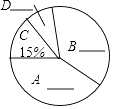
请你根据统计图、表提供的信息解答下列问题：
（1）这次抽样的公众有人．
（2）请将统计表和扇形统计图补充完整；
（3）在统计图中“B”部分所对应的圆心角是度．
（4）若该市有120万人，估计该市态度为“A．顾客出面制止”的有万人．

Answer 1

【答案】
（1）200
（2）解：如图所示

态度	A．顾客出面制止	B．劝说进吸烟室	C．超市老板出面制止	D．无所谓
频数（人数）	90	200	30	10

；

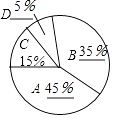（3）126
（4）45
【解析】解：（1）抽样的公众人数是30÷15%=200（人），

故答案是200；（2）B组的人数是200﹣90﹣30﹣10=70（人），

A组所占的百分比是 ×100%=45%，

B组所占的百分比是 ×100%=35%；

D组的百分比是 ×100%=5%．（3）在统计图中“B”部分所对应的圆心角是360°×36%=126°；（4）估计该市态度为“A．顾客出面制止”的有120×45%=54（万人）．

【考点精析】关于本题考查的扇形统计图，需要了解能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况才能得出正确答案．