
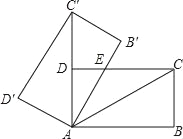
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为_____.
【答案】4![]()
【解析】分析:根据旋转后AC的中点恰好与D点重合,利用旋转的性质得到直角三角形ACD中,∠ACD=30°,再由旋转后矩形与已知矩形全等及矩形的性质得到∠DAE为30°,进而得到∠EAC=∠ECA,利用等角对等边得到AE=CE,设AE=CE=x,表示出AD与DE,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出EC的长,即可求出三角形AEC面积.
详解:∵旋转后AC的中点恰好与D点重合,即AD=![]() AC′=
AC′=![]() AC,
AC,
∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,
∴∠DAD′=60°,∴∠DAE=30°,
∴∠EAC=∠ACD=30°,∴AE=CE.
在Rt△ADE中,设AE=EC=x,
则有DE=DC﹣EC=AB﹣EC=6﹣x,AD=![]() ×6=2
×6=2![]() ,
,
根据勾股定理得:x2=(6﹣x)2+(2![]() )2,
)2,
解得:x=4,∴EC=4,
则S△AEC=![]() ECAD=4
ECAD=4![]() .
.
故答案为:4![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平面直角坐标系中的点A(a,1),t=ab﹣a2﹣b2(a,b是实数)
(1)若关于x的反比例函数y=![]() 过点A,求t的取值范围.
过点A,求t的取值范围.
(2)若关于x的一次函数y=bx过点A,求t的取值范围.
(3)若关于x的二次函数y=x2+bx+b2过点A,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
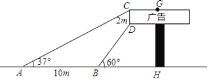
【题目】如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县古田镇某纪念品商店在销售中发现:“成功从这里开始”的纪念品平均每天可售出20件,每件盈利40元.为了扩大销售量,增加盈利,尽快减少库存,该商店在今年国庆黄金周期间,采取了适当的降价措施,改变营销策略后发现:如果每件降价4元,那么平均每天就可多售出8件.商店要想平均每天在销售这种纪念品上盈利1200元,那么每件纪念品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
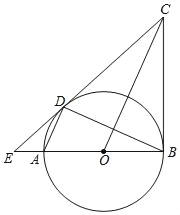
【题目】如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人走进一家商店,进门付l角钱,然后在店里购物花掉当时他手中钱的一半,走出商店付1角钱;之后,他走进第二家商店付1角钱,在店里花掉当时他手中钱的一半, 走出商店付1角钱;他又进第三家商店付l角钱,在店里花掉当时他手中钱的一半,出店付1角钱;最后他走进第四家商店付l角钱,在店里花掉当时他手中钱的一半, 出店付1角钱,这时他一分钱也没有了.该人原有钱的数目是________角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com